题目内容
15. 如图,在等腰△ABC中,AB=AC=9cm,BC=12cm,点D从B出发以每秒2cm的速度在线段BC上从B向C运动,点E同时从C出发以每秒2cm的速度在线段AC上从C向A运动,连接AD、DE.设运动时间为t秒,当∠ADE=90°-$\frac{1}{2}$∠BAC时,
如图,在等腰△ABC中,AB=AC=9cm,BC=12cm,点D从B出发以每秒2cm的速度在线段BC上从B向C运动,点E同时从C出发以每秒2cm的速度在线段AC上从C向A运动,连接AD、DE.设运动时间为t秒,当∠ADE=90°-$\frac{1}{2}$∠BAC时,(1)证明:∠ADE=∠B;
(2)求运动时间t的值.
分析 (1)根据三角形的内角和定理,等腰三角形的性质,可得答案;
(2)根据相似三角形的判定与性质,可得$\frac{AB}{DC}$=$\frac{BD}{CE}$,根据相似比,可得方程,根据解方程,可得答案.
解答 (1)证明:∵AB=AC=9cm,
∴∠B=∠C=$\frac{180°-∠BAC}{2}$,
即∠B=90°-$\frac{1}{2}$∠BAC,
∵∠ADE=90°-$\frac{1}{2}$∠BAC,
∴∠ADE=∠B;
(2)设运动t秒,BD=2t,CE=2t,
∵∠B=BDE,
∴∠BAD=∠CDE,
∵∠B=∠C,
∴△ABD∽△DCE,
∴$\frac{AB}{DC}$=$\frac{BD}{CE}$,
$\frac{9}{12-2x}$=$\frac{2x}{2x}$.
12-2x=9.
解得x=1.5,
答:运动时间为1.5秒.
点评 本题考查了相似三角形,利用了三角形内角和定理,相似三角形的判定与性质,利用相似三角形的相似比得出方程是解题关键.

练习册系列答案
相关题目
3.为了调查某小区居民的用水情况,随机抽查了若干户家庭月用水量,结果如表:
则关于这若干户家庭的月用水量,中位数是5吨,月平均用水4.6吨.
| 月用水量(吨) | 3 | 4 | 5 | 8 |
| 户数 | 2 | 3 | 5 | 1 |
 一个几何体的三视图如图,根据图示的数据计算该几何体的全面积是3π. (结果保留π).
一个几何体的三视图如图,根据图示的数据计算该几何体的全面积是3π. (结果保留π).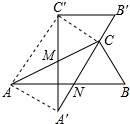 有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C=$\frac{1}{2}$,其中正确的有( )
有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C=$\frac{1}{2}$,其中正确的有( )
 如图,点B在线段AC上,点D、E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
如图,点B在线段AC上,点D、E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC. 如图,已知△ABC和点O,画出与△ABC关于点O对称的△A′B′C′.
如图,已知△ABC和点O,画出与△ABC关于点O对称的△A′B′C′. 如图所示,已知线段a、b、h(h<b).求作△ABC,使BC=a,AB=b,BC边上的高AD=h.(要求:写出作法,并保留作图痕迹)
如图所示,已知线段a、b、h(h<b).求作△ABC,使BC=a,AB=b,BC边上的高AD=h.(要求:写出作法,并保留作图痕迹)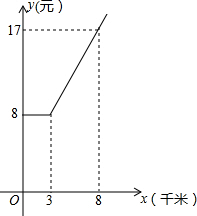 如图是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图,根据图象回答下列问题:
如图是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图,根据图象回答下列问题: