题目内容
5.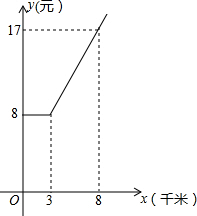 如图是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图,根据图象回答下列问题:
如图是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图,根据图象回答下列问题:(1)当出租车行使2千米时,收费应为8元;当出租车行使8千米时,收费应为17元.
(2)当出租车行使6千米时,收费应为$\frac{67}{5}$元;当收费为9.4元,出租车行使$\frac{34}{9}$千米.
(3)请写当x≥3时,出租车收费y(元)与行使路程x(千米)之间的函数关系?
分析 (1)由函数图象可以得出当出租车行使2千米时,收费应为8元;当出租车行使8千米时,收费应为17元;
(2)首先设当x≥3时,出租车单程收费y(元)与行驶路程x(千米)之间的函数关系式为y=kx+b,然后把(3,8),(8,17)代入可得关于k、b的二元一次方程组,再解可得k、b的值,进而可得函数解析式,然后再代入当x=6求出y;代入y=9.4,求出x即可;
(3)根据(2)的计算可得答案.
解答 解:(1)根据图象可得当出租车行使2千米时,收费应为8元;当出租车行使8千米时,收费应为17元.
故答案为:8;17;
(2)设当x≥3时,出租车单程收费y(元)与行驶路程x(千米)之间的函数关系式为y=kx+b,
∵图象经过(3,8),(8,17),
∴$\left\{\begin{array}{l}{8=3k+b}\\{17=8k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{9}{5}}\\{b=\frac{13}{5}}\end{array}\right.$,
∴函数解析式为y=$\frac{9}{5}$x+$\frac{13}{5}$,
当x=6时,y=$\frac{67}{5}$,
当y=9.4时,x=$\frac{34}{9}$,
故答案为:$\frac{67}{5}$;$\frac{34}{9}$;
(3)设当x≥3时,函数解析式为y=$\frac{9}{5}$x+$\frac{13}{5}$.
点评 此题主要考查了一次函数的应用,关键是正确理解题意,从图中获取正确信息,能利用待定系数法求出一次函数解析式.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
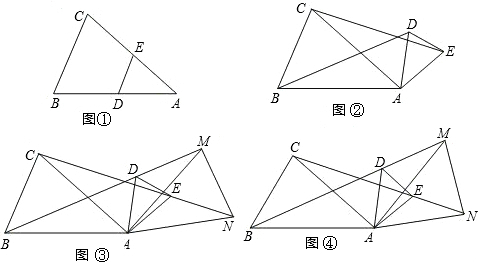
 如图,在等腰△ABC中,AB=AC=9cm,BC=12cm,点D从B出发以每秒2cm的速度在线段BC上从B向C运动,点E同时从C出发以每秒2cm的速度在线段AC上从C向A运动,连接AD、DE.设运动时间为t秒,当∠ADE=90°-$\frac{1}{2}$∠BAC时,
如图,在等腰△ABC中,AB=AC=9cm,BC=12cm,点D从B出发以每秒2cm的速度在线段BC上从B向C运动,点E同时从C出发以每秒2cm的速度在线段AC上从C向A运动,连接AD、DE.设运动时间为t秒,当∠ADE=90°-$\frac{1}{2}$∠BAC时, 按要求作图,并标出位置.
按要求作图,并标出位置. 如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为( )
如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为( )
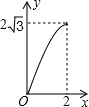
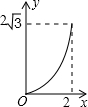
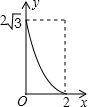
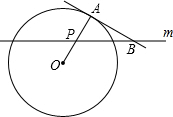 如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线m,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线m,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )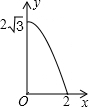
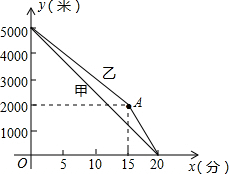 甲乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数的图象如图所示,根据图象所提供的信息解答下列问题:
甲乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数的图象如图所示,根据图象所提供的信息解答下列问题: