题目内容
1.某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.(1)求每件甲种、乙种玩具的进价分别是多少元.
(2)商场计划购进甲、乙两种玩具共48件,商场决定此次进货的总资金不超过1000元,那么甲种玩具最少购进多少个?
(3)在(2)的条件下,如果甲种玩具的件数少于乙种玩具的件数,求该商场最省钱的进货方案.
分析 (1)设甲种玩具进价x元/件,则乙种玩具进价为(40-x)元/件,根据已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同可列方程求解.
(2)设购进甲种玩具y件,则购进乙种玩具(48-y)件,根据商场决定此次进货的总资金不超过1000元,可列出不等式求解;
(3)结合(2)中所求,利用甲种玩具的件数少于乙种玩具的件数,得出y的取值,进而求出最值.
解答 解:(1)设甲种玩具进价x元/件,则乙种玩具进价为(40-x)元/件,根据题意可得:
$\frac{90}{x}$=$\frac{150}{40-x}$
解得:x=15,
经检验x=15是原方程的解.
故40-x=25.
答:甲,乙两种玩具分别是15元/件,25元/件;
(2)设购进甲种玩具y件,则购进乙种玩具(48-y)件,
15y+25(48-y)≤1000
解得:20≤y.
答:甲种玩具最少购进20个;
(3)∵y是整数,甲种玩具的件数少于乙种玩具的件数,
∴y<48-y,
解得:y<24
∴y取20,21,22,23,
方案一:购进甲种玩具20件,则购进乙种玩具28件,进货费用是20×15+28×25=1000(元).
方案二:购进甲种玩具21件,则购进乙种玩具27件,进货费用是21×15+27×25=990(元).
方案三:购进甲种玩具22件,则购进乙种玩具26件,进货费用是22×15+26×25=980(元).
方案四:购进甲种玩具23件,则购进乙种玩具25件,进货费用是23×15+25×25=970(元).
方案四的进货费用最低为970元.
点评 本题考查了列分式方程解实际问题的运用,分式方程的解法的运用,列不等式解方案设计问题的运用,正确不等关系是解题关键.

练习册系列答案
相关题目
12.计算-2×(210)的结果等于( )
| A. | -211 | B. | -410 | C. | 211 | D. | 411 |
9.已知△ABC和△A′B′C′是位似图形.△A′B′C′的面积为6cm2,△A′B′C′的周长是△ABC的周长一半.则△ABC的面积等于( )
| A. | 24cm2 | B. | 12cm2 | C. | 6cm2 | D. | 3cm2 |
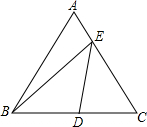 如图,在边长为4的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为2$\sqrt{7}$.
如图,在边长为4的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为2$\sqrt{7}$.