题目内容
11．当x＜0，化简$\sqrt{{x}^{4}+{x}^{2}{y}^{2}}$=-x$\sqrt{{x}^{2}+{y}^{2}}$．分析 直接利用x的取值范围，进而化简求出答案．
解答 解：∵x＜0，
∴$\sqrt{{x}^{4}+{x}^{2}{y}^{2}}$=-x$\sqrt{{x}^{2}+{y}^{2}}$．
故答案为：-x$\sqrt{{x}^{2}+{y}^{2}}$．
点评 此题主要考查了二次根式的化简，正确开平方是解题关键．
练习册系列答案
相关题目
2．一副完整的扑克牌，去掉大小王，将剩余的52张混合后从中随机抽取一张，则抽出A的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{12}$ | C． | $\frac{1}{13}$ | D． | $\frac{1}{52}$ |
16．若反比例函数y=$\frac{k}{x}$（k≠0）经过（-2，3），则这个反比例函数一定经过（ ）
| A． | （-2，-3） | B． | （3，2） | C． | （3，-2） | D． | （-3，-2） |
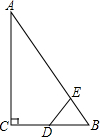如图，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，D为BC的中点，若动点E以1cm/s的速度从A点出发，沿着A→B的方向运动，设E点的运动时间为t秒，连接DE，当△BDE是直角三角形时，t的值为2或3.5．