题目内容
9.已知△ABC和△A′B′C′是位似图形.△A′B′C′的面积为6cm2,△A′B′C′的周长是△ABC的周长一半.则△ABC的面积等于( )| A. | 24cm2 | B. | 12cm2 | C. | 6cm2 | D. | 3cm2 |
分析 根据位似变换的性质、相似三角形的性质计算即可.
解答 解:∵△A′B′C′的周长是△ABC的周长一半,
∴△A′B′C′与△ABC的相似比为1:2,
∴△A′B′C′与△ABC的面积比为1:4,
∴△ABC的面积为24cm2,
故选:A.
点评 本题考查的是位似变换的性质、相似三角形的性质,掌握位似图形的定义:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形是解题的关键.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
4.互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品进价为200元,按标价的五折销售,仍可获利10%,设这件商品的标价为x元,根据题意列出方程( )
| A. | 0.5x-200=10%×200 | B. | 0.5x-200=10%×0.5x | ||
| C. | 200=(1-10%)×0.5x | D. | 0.5x=(1-10%)×200 |
18.计算下列各式的值
(1)$\sqrt{25}$-$\root{3}{-27}$+$\sqrt{(-7)^{2}}$
(2)|-$\sqrt{2}$|+|$\sqrt{2}$-$\sqrt{3}$|.
(1)$\sqrt{25}$-$\root{3}{-27}$+$\sqrt{(-7)^{2}}$
(2)|-$\sqrt{2}$|+|$\sqrt{2}$-$\sqrt{3}$|.
19.要使$\sqrt{x-5}$有意义,x的取值范围是( )
| A. | x≥5 | B. | x≤5 | C. | x>5 | D. | x<5 |
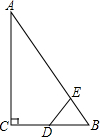 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值为2或3.5.
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值为2或3.5.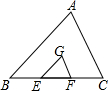 如图,点G是△ABC的重心,过G作GE∥AB,交BC于E,GF∥AC,交BC于F,则S△GEF:S△ABC=1:9.
如图,点G是△ABC的重心,过G作GE∥AB,交BC于E,GF∥AC,交BC于F,则S△GEF:S△ABC=1:9.