题目内容
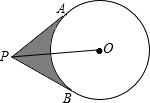 如图,已知P为⊙O外一点,PA、PB切⊙O于A、B两点,PO=4cm,∠APB=60°,求阴影部分的周长与面积.
如图,已知P为⊙O外一点,PA、PB切⊙O于A、B两点,PO=4cm,∠APB=60°,求阴影部分的周长与面积.考点:切线的性质,扇形面积的计算
专题:
分析:连接OA、OB,根据切线的性质定理求得∠AOB的度数,然后根据弧长公式求得弧AB的长,根据三角形求得PA和PB的长,则阴影部分的周长即可求得;四边形OABB的面积是△OPA的面积的2倍,然后减去扇形OAB的面积即可求得阴影部分的面积.
解答: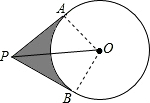 解:连接OA、OB.
解:连接OA、OB.
∵PA、PB切⊙O于A、B两点,
∴∠OAP=∠OBP=90°,∠APO=
∠APB=30°,
∴OA=
OP=2cm,∠AOB=120°,
∴PA=PB=OP•sin60°=4×
=2
(cm),
弧AB的长是:
=
(cm),
则阴影部分的周长是:2×2
+
=4
+
;
S△OPA=
OA•PA=
×2×2
=2
,
则S四边形OAPB=4
,
又S扇形OAB=
=
,
则S阴影=4
-
(cm2).
 解:连接OA、OB.
解:连接OA、OB.∵PA、PB切⊙O于A、B两点,
∴∠OAP=∠OBP=90°,∠APO=
| 1 |
| 2 |
∴OA=
| 1 |
| 2 |
∴PA=PB=OP•sin60°=4×
| ||
| 2 |
| 3 |
弧AB的长是:
| 120π×2 |
| 180 |
| 4π |
| 3 |
则阴影部分的周长是:2×2
| 3 |
| 4π |
| 3 |
| 3 |
| 4π |
| 3 |
S△OPA=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
则S四边形OAPB=4
| 3 |
又S扇形OAB=
| 120π×22 |
| 360 |
| 4π |
| 3 |
则S阴影=4
| 3 |
| 4π |
| 3 |
点评:本题考查了切线的性质定理以及扇形和弧长的计算公式,正确求得圆的半径OA的长以及圆心角∠AOB的度数是关键.

练习册系列答案
相关题目
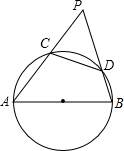 如图,已知圆的直径,AB=6cm,CD是圆上长为2cm的弦,当弦CD在半圆AB上滑动时,AC和BD延长线的夹角是否为定值?如果不是,说明理由;如果是,求出这个定角的正弦值.
如图,已知圆的直径,AB=6cm,CD是圆上长为2cm的弦,当弦CD在半圆AB上滑动时,AC和BD延长线的夹角是否为定值?如果不是,说明理由;如果是,求出这个定角的正弦值.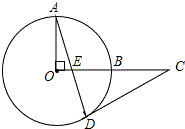 如图,OA、OB是⊙O的半径,OA⊥OB,点C是OB延长线上一点,过点C作⊙O的切线,点D是切点,连接AD交OB于点E.求证:CD=CE.
如图,OA、OB是⊙O的半径,OA⊥OB,点C是OB延长线上一点,过点C作⊙O的切线,点D是切点,连接AD交OB于点E.求证:CD=CE.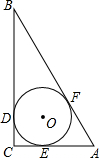 如图,在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm.
如图,在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm. 如图,在△ABC中,AD为BC边上的中线,AE:ED=1:2,连结BE并延长交AC于点F.若AF=4,求CF的长.
如图,在△ABC中,AD为BC边上的中线,AE:ED=1:2,连结BE并延长交AC于点F.若AF=4,求CF的长.