题目内容
如图，在△ABC中，AD为BC边上的中线，AE：ED=1：2，连结BE并延长交AC于点F．若AF=4，求CF的长．考点：平行线分线段成比例,三角形中位线定理
专题：
分析：如图，作辅助线；由DG∥BF，得到AE：ED=AF：FG；结合AE：ED=1：2，AF=4，求出FG的长度；证明CG=FG即可解决问题．
解答：
解：如图，过点D作DG∥BF，交AC于点G；
则AE：ED=AF：FG，而AE：ED=1：2，AF=4，
∴FG=8；
∵AD为BC边上的中线，且DG∥BF，
∴CG=FG=8，
∴CF=16．
解：如图，过点D作DG∥BF，交AC于点G；则AE：ED=AF：FG，而AE：ED=1：2，AF=4，
∴FG=8；
∵AD为BC边上的中线，且DG∥BF，
∴CG=FG=8，
∴CF=16．
点评：该题主要考查了平行线分线段成比例定理及其应用问题；解题的关键是作辅助线，灵活运用定理来分析、解答．
练习册系列答案
相关题目
一个物体的三视图如图所示，请画出该物体的形状．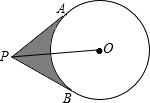
如图，已知P为⊙O外一点，PA、PB切⊙O于A、B两点，PO=4cm，∠APB=60°，求阴影部分的周长与面积．
甲，乙两人在直线跑道上同起点，同终点，同方向匀速跑步500m，先到终点的人原地休息，已知甲先出发2秒，在在跑步过程中，甲、乙两人的距离y（米）与乙出发的时间t（秒）之间的关系如图所示，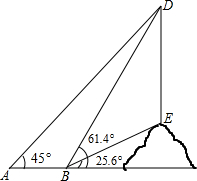
如图，课外数学小组要测量小山坡上塔的高度DE，DE所在直线与水平线AN垂直．他们在A处测得塔尖D的仰角为45°，再沿着射线AN方向前进50米到达B处，此时测得塔尖D的仰角∠DBN=25.6°．现在请你帮助课外活动小组算一算塔高DE大约是多少米？（结果精确到个位）（参考数据：sin25.6°≈0.4，cos25.6°≈0.9，tan25.6°≈0.5，sin61.4°≈0.9，cos61.4°≈0.5，tan61.4°≈1.8）