题目内容
11.在四边形ABCD中,∠B+∠D=180°,对角线AC平分∠BAD.(1)如图1,若∠DAB=120°,且∠B=90°,试探究边AD、AB与对角线AC的数量关系并说明理由.
(2)如图2,若将(1)中的条件“∠B=90°”去掉,(1)中的结论是否成立?请说明理由.
(3)如图3,若∠DAB=90°,探究边AD、AB与对角线AC的数量关系并说明理由.
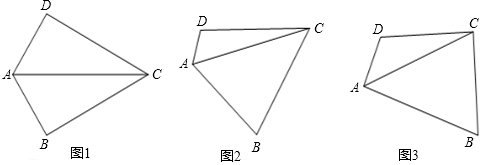
分析 (1)结论:AC=AD+AB,只要证明AD=$\frac{1}{2}$AC,AB=$\frac{1}{2}$AC即可解决问题;
(2)(1)中的结论成立.以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,只要证明△DAC≌△BEC即可解决问题;
(3)结论:$AD+AB=\sqrt{2}AC$.过点C作CE⊥AC交AB的延长线于点E,只要证明△ACE是等腰直角三角形,△DAC≌△BEC即可解决问题;
解答 解:(1)AC=AD+AB.
理由如下:如图1中,
在四边形ABCD中,∠D+∠B=180°,∠B=90°,
∴∠D=90°,
∵∠DAB=120°,AC平分∠DAB,
∴∠DAC=∠BAC=60°,
∵∠B=90°,
∴$AB=\frac{1}{2}AC$,同理$AD=\frac{1}{2}AC$.
∴AC=AD+AB.
(2)(1)中的结论成立,理由如下:以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,
∵∠BAC=60°,
∴△AEC为等边三角形,
∴AC=AE=CE,
∵∠D+∠B=180°,∠DAB=120°,
∴∠DCB=60°,
∴∠DCA=∠BCE,
∵∠D+∠ABC=180°,∠ABC+∠EBC=180°,
∴∠D=∠CBE,∵CA=CB,
∴△DAC≌△BEC,
∴AD=BE,
∴AC=AD+AB.
(3)结论:$AD+AB=\sqrt{2}AC$.理由如下:
过点C作CE⊥AC交AB的延长线于点E,∵∠D+∠B=180°,∠DAB=90°,
∴DCB=90°,
∵∠ACE=90°,
∴∠DCA=∠BCE,
又∵AC平分∠DAB,
∴∠CAB=45°,
∴∠E=45°.
∴AC=CE.
又∵∠D+∠B=180°,∠D=∠CBE,
∴△CDA≌△CBE,
∴AD=BE,
∴AD+AB=AE.
在Rt△ACE中,∠CAB=45°,
∴$AE=\frac{AC}{{cos{{45}°}}}=\sqrt{2}AC$,
∴$AD+AB=\sqrt{2}AC$.
点评 本题考查四边形综合题、等边三角形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

| A. | 83×10 | B. | 8.3×102 | C. | 8.3×103 | D. | 0.83×103 |
 如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB、CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB、CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )| A. | 2米 | B. | 2.5米 | C. | 2.4米 | D. | 2.1米 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
| A. | 9 | B. | -9 | C. | 3 | D. | -3 |
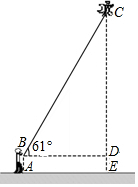 小蓝周末去广场放风筝,如图,当风筝飞到点C处时的线长BC约为25m,此时小蓝正好站在点A处,并测得∠CBD=61°,牵引底端B距离地面1.5m,则此时风筝距离地面的高度CE约为23.3m(用科学计算器计算,结果精确到0.1m).
小蓝周末去广场放风筝,如图,当风筝飞到点C处时的线长BC约为25m,此时小蓝正好站在点A处,并测得∠CBD=61°,牵引底端B距离地面1.5m,则此时风筝距离地面的高度CE约为23.3m(用科学计算器计算,结果精确到0.1m).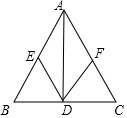 如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.
如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.