题目内容
16.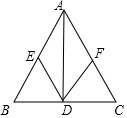 如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.
如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.(1)求证:四边形AEDF是菱形;
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积S.
分析 (1)先根据直角三角形斜边上中线的性质,得出DE=$\frac{1}{2}$AB=AE,DF=$\frac{1}{2}$AC=AF,再根据AB=AC,点E、F分别是AB、AC的中点,即可得到AE=AF=DE=DF,进而判定四边形AEDF是菱形;
(2)设EF=x,AD=y,则x+y=7,进而得到x2+2xy+y2=49,再根据Rt△AOE中,AO2+EO2=AE2,得到x2+y2=36,据此可得xy=$\frac{13}{2}$,进而得到菱形AEDF的面积S.
解答 解:(1)∵AD⊥BC,点E、F分别是AB、AC的中点,
∴Rt△ABD中,DE=$\frac{1}{2}$AB=AE,
Rt△ACD中,DF=$\frac{1}{2}$AC=AF,
又∵AB=AC,点E、F分别是AB、AC的中点,
∴AE=AF,
∴AE=AF=DE=DF,
∴四边形AEDF是菱形;
(2)如图,∵菱形AEDF的周长为12,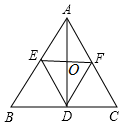
∴AE=3,
设EF=x,AD=y,则x+y=7,
∴x2+2xy+y2=49,①
∵AD⊥EF于O,
∴Rt△AOE中,AO2+EO2=AE2,
∴($\frac{1}{2}$y)2+($\frac{1}{2}$x)2=32,
即x2+y2=36,②
把②代入①,可得2xy=13,
∴xy=$\frac{13}{2}$,
∴菱形AEDF的面积S=$\frac{1}{2}$xy=$\frac{13}{4}$.
点评 本题主要考查了菱形的判定与性质的运用,解题时注意:四条边相等的四边形是菱形;菱形的面积等于对角线长乘积的一半.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
6.下列调查中,适合采用全面调查方式的是( )
| A. | 了解一批灯管的使用寿命 | B. | 了解居民对废电池的处理情况 | ||
| C. | 了解一个班级的数学考试成绩 | D. | 了解全国七年级学生的视力情况 |
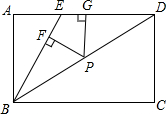 如图,E为矩形ABCD边AD上的一点,BE=ED,P为对角线BD上任一点,PF⊥BE,PG⊥AD,垂足分别为F、G,且AB=2cm,求PF+PG=2.
如图,E为矩形ABCD边AD上的一点,BE=ED,P为对角线BD上任一点,PF⊥BE,PG⊥AD,垂足分别为F、G,且AB=2cm,求PF+PG=2.