题目内容
8.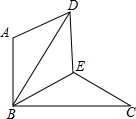 如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
分析 (1)根据旋转的性质可得DB=CB,∠ABD=∠EBC,∠ABE=60°,然后根据垂直可得出∠DBE=∠CBE=30°,继而可根据SAS证明△BDE≌△BCE;
(2)根据(1)以及旋转的性质可得,△BDE≌△BCE≌△BDA,继而得出四条棱相等,证得四边形ABED为菱形.
解答 (1)证明:∵△BAD是由△BEC在平面内绕点B旋转60°而得,
∴DB=CB,∠ABD=∠EBC,∠ABE=60°,
∵AB⊥EC,
∴∠ABC=90°,
∴∠DBE=∠CBE=30°,
在△BDE和△BCE中,
∵$\left\{\begin{array}{l}{DB=CB}\\{∠DBE=∠CBE}\\{BE=BE}\end{array}\right.$,
∴△BDE≌△BCE;
(2)四边形ABED为菱形;
由(1)得△BDE≌△BCE,
∵△BAD是由△BEC旋转而得,
∴△BAD≌△BEC,
∴BA=BE,AD=EC=ED,
又∵BE=CE,
∴四边形ABED为菱形.
点评 本题考查了旋转的性质,解答本题的关键是掌握全等三角形的判定和性质以及菱形的判定,涉及知识点较多,难度较大.

练习册系列答案
相关题目
18.位似图形的位似中心可以在( )
| A. | 原图形外 | B. | 原图形内 | C. | 原图形的边上 | D. | 以上三种都可以 |
19.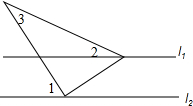 如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )
如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )
 如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )
如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )| A. | 26°40′ | B. | 27°20′ | C. | 27°40′ | D. | 73°20′ |
16.下列各数中最小的是( )
| A. | -5 | B. | -4 | C. | 3 | D. | 4 |
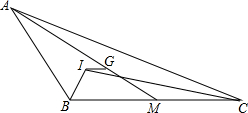 如图,在△ABC中,∠ABC、∠ACB的平分线交于点I,AM是BC上的中线,G为AM上一点,AG:GM=2:1,IG∥BC.求证:AB+AC=2BC.
如图,在△ABC中,∠ABC、∠ACB的平分线交于点I,AM是BC上的中线,G为AM上一点,AG:GM=2:1,IG∥BC.求证:AB+AC=2BC.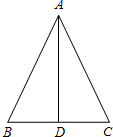 已知,△ANC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,求:
已知,△ANC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,求: