题目内容
20.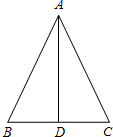 已知,△ANC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,求:
已知,△ANC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,求:①△ABC的面积;
②试求△ABC中AB边上的高.
分析 (1)利用三边之间关系,可知三角形ABD是直角三角形,得出AD是高,可求△ABC的面积;
(2)再进一步利用△ABC的面积求△ABC中AB边上的高.
解答 解:(1)∵AD是中线,
∴BD=$\frac{1}{2}$BC=8,
∵BD2+AD2=64+225=289=AB2,
∴三角形ABD是直角三角形,且AD是高.
∴△ABC的面积=$\frac{1}{2}$BC×AD=$\frac{1}{2}$×16×15=120cm2.
(2)△ABC中AB边上的高=120×2÷17=$\frac{240}{17}$cm.
点评 此题考查勾股定理逆定理与三角形面积计算方法的运用,利用勾股定理逆定理判定△ABD是直角三角形是解决问题的关键.

练习册系列答案
相关题目
5.既不是正数,也不是负数的数是( )
| A. | 1 | B. | 0 | C. | π | D. | $\frac{1}{3}$ |
12.上午9时,一艘船从A处出发以每小时20海里的速度向正北方向航行,11时到达B处,若在A处测得灯塔C在北偏西34°,且∠ACB=$\frac{3}{2}$∠BAC,则在B处测得灯塔C应为( )
| A. | 北偏西68° | B. | 南偏西85° | C. | 北偏西85° | D. | 南偏西68° |
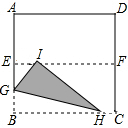 如图,将边长为4的正方形ABCD对折后展开,折痕为EF,分别在边AB、BC上取点G、H,沿GH对折,使点B落在折痕EF上,落点记为I,则:
如图,将边长为4的正方形ABCD对折后展开,折痕为EF,分别在边AB、BC上取点G、H,沿GH对折,使点B落在折痕EF上,落点记为I,则:
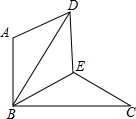 如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.