题目内容
13.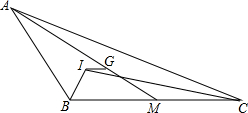 如图,在△ABC中,∠ABC、∠ACB的平分线交于点I,AM是BC上的中线,G为AM上一点,AG:GM=2:1,IG∥BC.求证:AB+AC=2BC.
如图,在△ABC中,∠ABC、∠ACB的平分线交于点I,AM是BC上的中线,G为AM上一点,AG:GM=2:1,IG∥BC.求证:AB+AC=2BC.
分析 延长IG交AC于F,延长GI交AB于E,得到EF∥BC,根据平行线的性质得到∠EIB=∠EBI,∠FIC=∠FCI,根据角平分线的性质得到∠EBI=∠IBM.∠FCI=∠ICM,等量代换得到∠EIB=∠EBI,∠FIC=∠FCI,求得EF=EI+IF=BE+CF,然后根据平行线分线段成比例即可得到结论.
解答 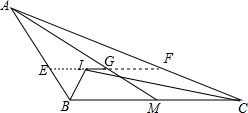 解:延长IG交AC于F,延长GI交AB于E,
解:延长IG交AC于F,延长GI交AB于E,
∵IG∥BC,
∴EF∥BC,
∴∠EIB=∠EBI,∠FIC=∠FCI,
∵BI,CI分别平分∠ABC、∠ACB,
∴∠EBI=∠IBM.∠FCI=∠ICM,
∴∠EIB=∠EBI,∠FIC=∠FCI,
∴EI=EB,FI=FC,
∴EF=EI+IF=BE+CF,
∵AG:GM=2:1,
∴AM:GM=3:1,
∵EF∥BC,
∴$\frac{AB}{BE}=\frac{AC}{CF}$=3,
∴BE=$\frac{1}{3}$AB,CF=$\frac{1}{3}$AC,
∴BE+CF=$\frac{1}{3}$(AB+AC),
∴$\frac{EF}{BC}=\frac{AE}{AB}=\frac{2}{3}$,
∴EF=$\frac{2}{3}$BC,
∴EF=BE+CF=$\frac{1}{3}$(AB+AC)=$\frac{2}{3}$BC,
∴AB+AC=2BC.
点评 本题考查了平行线分线段成比例定理,角平分线的性质,等腰三角形的判定,熟练掌握平行线分线段成比例定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.下列命题是真命题的是( )
| A. | 任何数的0次幂都等于1 | |
| B. | 顺次连接菱形四边中点的线段组成的四边形是正方形 | |
| C. | 图形的旋转和平移会改变图形的形状和大小 | |
| D. | 角平分线上的点到角两边的距离相等 |
5.既不是正数,也不是负数的数是( )
| A. | 1 | B. | 0 | C. | π | D. | $\frac{1}{3}$ |
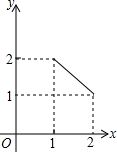
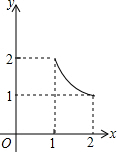
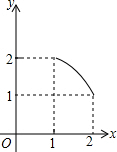
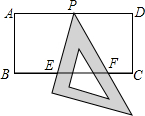 如图,在矩形ABCD中,AD=2,AB=1,P是AD的中点,等腰直角三角板45°角的顶点与点P重合,当此三角板绕点P旋转时,它的直角边和斜边所在的直线与BC分别相交于E、F两点.设线段BF=x,CE=y,则下列图象中,能表示y与x的函数关系的大致图象是( )
如图,在矩形ABCD中,AD=2,AB=1,P是AD的中点,等腰直角三角板45°角的顶点与点P重合,当此三角板绕点P旋转时,它的直角边和斜边所在的直线与BC分别相交于E、F两点.设线段BF=x,CE=y,则下列图象中,能表示y与x的函数关系的大致图象是( )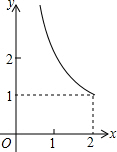
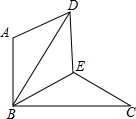 如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.