题目内容
10. 如图,∠ACB=80°,CA=CB,点E、F分别是直线CD上的两点,且∠BEC=∠CFA=100°,求证:BE=EF+AF.
如图,∠ACB=80°,CA=CB,点E、F分别是直线CD上的两点,且∠BEC=∠CFA=100°,求证:BE=EF+AF.
分析 根据三角形的内角和定理可得∠BCE+∠BEC+∠CBE=180°,从而得到∠CBE=∠ACF,再利用“AAS”证明△BCE和△CAF全等,根据全等三角形对应边相等可得BE=CF,AF=CE,从而得证.
解答 证明:在△BCE中,∠BCE+∠BEC+∠CBE=180°,
∵∠BCA+∠BEC=180°,
∴∠CBE=∠ACF,
在△BCE和△CAF中,
$\left\{\begin{array}{l}{∠CBE=∠ACF}\\{∠BEC=∠CFA}\\{CA=CB}\end{array}\right.$,
∴△BCE≌△CAF(AAS),
∴BE=CF,AF=CE,
∴BE=EF+AF.
点评 本题考查了全等三角形的判定与性质,三角形的内角和定理,熟练掌握三角形全等的判断方法并求出∠CBE=∠ACF是解题的关键.

练习册系列答案
相关题目
1.按某种标准把多项式进行分类时,3x3-4和a2b+ab2+1属于同一类,则下列哪一个多项式也属于这一类( )
| A. | -x3+y5 | B. | 2x2-3 | C. | abc-1 | D. | a2+2ab+b2 |
 如图,已知BO、C0分别是∠ABC和∠ACB的平分线,OE∥AB、OF∥AC,如果已知BC的长为a,你能知道△OEF的周长吗?算算看.
如图,已知BO、C0分别是∠ABC和∠ACB的平分线,OE∥AB、OF∥AC,如果已知BC的长为a,你能知道△OEF的周长吗?算算看. 如图,在△ABC中,AD为BC的中线,AB=AC,求证:点D在∠BAC的平分线上.
如图,在△ABC中,AD为BC的中线,AB=AC,求证:点D在∠BAC的平分线上.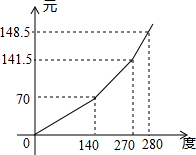 武汉市2012年4月居民用电准备实行阶梯电价,第一档为140°以内价格不变,第二档为140°-270°价格微调,第三档超过270°以上价格再加一点,每个月的电费y(元)与用电量x(度)的函数关系如图所示,若某居民9月份用电300度,电费调整后将多支出12.5元.
武汉市2012年4月居民用电准备实行阶梯电价,第一档为140°以内价格不变,第二档为140°-270°价格微调,第三档超过270°以上价格再加一点,每个月的电费y(元)与用电量x(度)的函数关系如图所示,若某居民9月份用电300度,电费调整后将多支出12.5元.