题目内容
16. 如图,E,F是四边形ABCD的对角线BD上的两点,AB=CD,AD=CB,DF=BE.求证:AE∥CF.
如图,E,F是四边形ABCD的对角线BD上的两点,AB=CD,AD=CB,DF=BE.求证:AE∥CF.
分析 由平行四边形的性质可知:∠ABE=∠CDF,再利用已知条件和三角形全等的判定方法即可证明△ABE≌△CDF,所以∠AEB=∠DFC,进而可得∠AED=∠BFC,所以AE∥CF.
解答 证明:∵AB=CD,AD=CB,
∴四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∴∠ABE=∠CDF,
在△ABE和△CDF中,
∵$\left\{\begin{array}{l}{AB=CD}\\{∠ABE=∠CDF}\\{BE=DF}\end{array}\right.$,
∴△ABE≌△CDF(SAS),
∴∠AEB=∠DFC,AE=CF,
∴∠AED=∠BFC,
∴AE∥CF.
点评 本题考查了全等三角形的判定和性质,关键是根据平行四边形的性质、全等三角形的判定和性质以及平行线的判定方法解答.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 在Rt△ABC中,∠C=90°,M是AB的中点,PM⊥MQ.P、Q分别在边AC、BC上.
在Rt△ABC中,∠C=90°,M是AB的中点,PM⊥MQ.P、Q分别在边AC、BC上.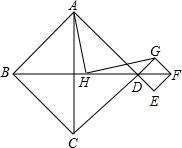 四边形ABCD与四边形DEFG都是正方形,点H为BF的中点,连接HA,HG.若三点B、D、F在同一直线上,如图探索HA与HG的数量及位置关系,并予以证明.
四边形ABCD与四边形DEFG都是正方形,点H为BF的中点,连接HA,HG.若三点B、D、F在同一直线上,如图探索HA与HG的数量及位置关系,并予以证明. 如图,抛物线y=ax2+bx+c(a≠0)交x轴于点A,点B,交y轴于点E,其中B点的坐标为(3,0),OB=3OA,连接AE,tan∠EAO=3,直线y=-2x-2交x轴于点C,交y轴于点D.
如图,抛物线y=ax2+bx+c(a≠0)交x轴于点A,点B,交y轴于点E,其中B点的坐标为(3,0),OB=3OA,连接AE,tan∠EAO=3,直线y=-2x-2交x轴于点C,交y轴于点D.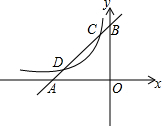 如图所示,已知直线y1=x+m与x轴、y轴分别交于点A,B,与反比例函数y2=$\frac{k}{x}$(x<0)的图象分别交于点C、D,且C的坐标为(-1,2)
如图所示,已知直线y1=x+m与x轴、y轴分别交于点A,B,与反比例函数y2=$\frac{k}{x}$(x<0)的图象分别交于点C、D,且C的坐标为(-1,2)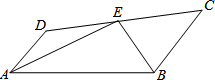 如图:E在线段CD上,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°.设AD=x,BC=y,且(x-3)2+|y-4|=0,AB的长度是( )
如图:E在线段CD上,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°.设AD=x,BC=y,且(x-3)2+|y-4|=0,AB的长度是( )