题目内容
5. 如图,在?ABCD中,O是对角线AC,BD的交点,已知AB=4,△AOB的周长是11,则AC+BD=14.
如图,在?ABCD中,O是对角线AC,BD的交点,已知AB=4,△AOB的周长是11,则AC+BD=14.
分析 根据平行四边形对角线互相平分可得AO=$\frac{1}{2}$AC,BO=$\frac{1}{2}$BD,再由△AOB的周长是11可得AO+BO的长,进而可得答案.
解答 解:∵四边形ABCD是平行四边形,
∴AO=$\frac{1}{2}$AC,BO=$\frac{1}{2}$BD,
∵AB=4,△AOB的周长是11,
∴AO+BO=11-4=7,
∴AC+BD=14,
故答案为:14.
点评 此题主要考查了平行四边形的性质,关键是掌握平行四边形对角线互相平分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
如图,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
 如图,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
如图,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )| A. | 2.5 | B. | 1.5 | C. | 4 | D. | 5 |
17.在下列方程中,是一元二次方程的是( )
| A. | x2+3x=$\frac{2}{x}$ | B. | 2(x-1)+x=2 | C. | x2=2+3x | D. | x2-x3+4=0 |
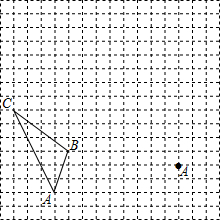 如图,在边长为1个单位长度的小正方形组成的网格中,
如图,在边长为1个单位长度的小正方形组成的网格中, 如图,A、B分别是x轴、y轴上的点,A(3,0)、B(0,4);分别以OB、AB为边作等边△OBD、△ABD.
如图,A、B分别是x轴、y轴上的点,A(3,0)、B(0,4);分别以OB、AB为边作等边△OBD、△ABD. 如图,?ABCD中,延长DB至点E,延长BD至点F,使得BE=DF,连结AE,EC,CF,FA.求证:四边形AECF是平行四边形.
如图,?ABCD中,延长DB至点E,延长BD至点F,使得BE=DF,连结AE,EC,CF,FA.求证:四边形AECF是平行四边形.