题目内容
5.已知抛物线顶点为(2,3),且过点(1,1),求抛物线解析式.分析 设抛物线的顶点式为y=a(x-h)2+k,由顶点坐标可知:h=-2,k=3,最后将(1,1)代入抛物线的解析式即可求出a的值.
解答 解:设抛物线的顶点式为y=a(x-h)2+k,
由顶点坐标可知:h=2,k=3,
∴抛物线的解析式为:y=a(x-2)2+3
将(1,1)代入上式,
∴1=a+3
∴a=-2
∴抛物线的解析式为:y=-2(x-2)2+3
点评 本题考查待定系数法求解析式,解题的关键是设抛物线的解析式为顶点式,然后通过顶点坐标和(1,1)求出a、h、k的值,本题属于基础题型.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
10.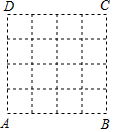 在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在各点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.
在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在各点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.
 在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在各点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.
在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在各点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
17.如果$\frac{a}{b}$=2,则$\frac{{a}^{2}-ab+{b}^{2}}{{a}^{2}+{b}^{2}}$的值等于( )
| A. | $\frac{4}{5}$ | B. | 1 | C. | $\frac{3}{5}$ | D. | 2 |
 按要求完成下列问题:
按要求完成下列问题: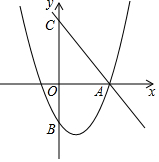 如图,直线y=-$\frac{4}{3}$x+4交x轴于点A,交y轴于点C,抛物线y=ax2-$\frac{4}{3}$x+c过点A,交y轴于点B(0,-2).
如图,直线y=-$\frac{4}{3}$x+4交x轴于点A,交y轴于点C,抛物线y=ax2-$\frac{4}{3}$x+c过点A,交y轴于点B(0,-2).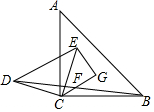 如图,△ABC和△DEC都是等腰直角三角形,连接BD,F是BD的中点,连接CF并延长至G,使FG=CF,连接EC,CE=10,CF=4,EG=6,则S△ABC=2$\sqrt{130}$.
如图,△ABC和△DEC都是等腰直角三角形,连接BD,F是BD的中点,连接CF并延长至G,使FG=CF,连接EC,CE=10,CF=4,EG=6,则S△ABC=2$\sqrt{130}$.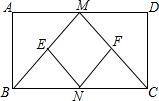 如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点
如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点