Question

4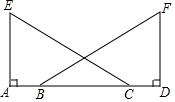．已知：如图，点A，B，C，D同一条直线上，EA⊥AD，FD⊥AD，AE=DF，AB=DC．问：∠ACE=∠DBF吗？说明理由．

Answer 1

分析 根据EA⊥AD，FD⊥AD，得出∠EAD=∠FDB，再根据AB=DC得出AC=BD，最后根据SAS证出△EAC≌△FDB，即可得出∠ACE=∠DBF．

解答 解：∵EA⊥AD，FD⊥AD，
∴∠EAD=∠FDB=90°，
又∵AB=DC，
∴AB+BC=DC+BC，
即AC=BD，
又∵AE=DF，
在△EAC和△FDB中，
$\left\{\begin{array}{l}{AE=DF}\\{∠EAD=∠FDB}\\{AC=BD}\end{array}\right.$，
∴△EAC≌△FDB，
∴∠ACE=∠DBF．

点评 本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．证明角、边相等常常运三角形全等来证明．