题目内容
15.先化简,再求值:[(x-2y)2-(-x-2y)(-x+2y)]÷(-4y),其中x和y的取值满足$\sqrt{{x}^{2}-2x+1}$+(x2+4xy+4y2)=0.
分析 先化简,然后根据非负数的性质得出x、y的值,将x与y的值求出代入.
解答 解:原式=(x2-4xy+4y2-x2+4y2)÷4y
=(-4xy+8y2)÷4y
=-x+2y
∵$\sqrt{{x}^{2}-2x+1}$+(x2+4xy+4y2)=0,即|x-1|+(x+2y)2=0,
∴x-1=0,x+2y=0,
∴x=1,y=-$\frac{1}{2}$,
则原式=-1+2×(-$\frac{1}{2}$)=-1-1=-2.
点评 本题主要考查整式的化简求值及非负数的性质,熟练掌握整式的混合运算顺序和运算法则及根据非负数性质得出x、y的值是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
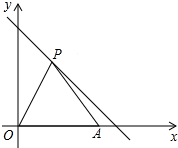 如图,点A坐标为(4,0),点P在第一象限且在直线y=-x+5上.
如图,点A坐标为(4,0),点P在第一象限且在直线y=-x+5上.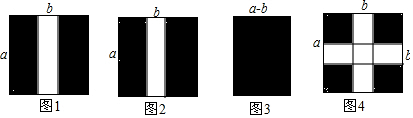
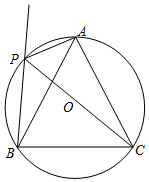 如图,⊙O是等边三角形ABC的外接圆,点P是$\widehat{AB}$上一点,连接AP,CP,作射线BP.
如图,⊙O是等边三角形ABC的外接圆,点P是$\widehat{AB}$上一点,连接AP,CP,作射线BP.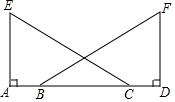 已知:如图,点A,B,C,D同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.问:∠ACE=∠DBF吗?说明理由.
已知:如图,点A,B,C,D同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.问:∠ACE=∠DBF吗?说明理由. 结合如下面积为3的正方形,在数轴上表示±$\sqrt{3}$.
结合如下面积为3的正方形,在数轴上表示±$\sqrt{3}$.