题目内容
19.观察下列运算:$\frac{1}{1+\sqrt{2}}$=$\sqrt{2}$-1,$\frac{1}{\sqrt{2}+\sqrt{3}}$=$\sqrt{3}$-$\sqrt{2}$,$\frac{1}{\sqrt{3}+\sqrt{4}}$=$\sqrt{4}$-$\sqrt{3}$,…,$\frac{1}{\sqrt{2016}+\sqrt{2017}}$=$\sqrt{2017}$-$\sqrt{2016}$请回答下列问题:
(1)观察上面解题过程,直接写出下面式子的结果
$\frac{1}{\sqrt{9}+\sqrt{10}}$=$\sqrt{10}-\sqrt{9}$;$\frac{1}{\sqrt{n}+\sqrt{n+1}}$=$\sqrt{n+1}-\sqrt{n}$(n≥1)
(2)利用上面规律计算:
($\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2016}+\sqrt{2017}}$)(1+$\sqrt{2017}$)
分析 (1)根据题意利用平方差公式分母有理化可以解答本题;
(2)根据题目中的信息利用平方差公式分母有理化,再利用平方差公式可以解答本题.
解答 解:(1)由题意可得,
$\frac{1}{\sqrt{9}+\sqrt{10}}=\sqrt{10}-\sqrt{9}$,$\frac{1}{\sqrt{n}+\sqrt{n+1}}=\sqrt{n+1}-\sqrt{n}$;
(2)($\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2016}+\sqrt{2017}}$)(1+$\sqrt{2017}$)
=($\sqrt{2}-1+\sqrt{3}-\sqrt{2}+\sqrt{4}-\sqrt{3}+…+\sqrt{2017}-\sqrt{2016}$)(1+$\sqrt{2017}$)
=($\sqrt{2017}-1$)($\sqrt{2017}+1$)
=2017-1
=2016.
故答案为:$\sqrt{10}-\sqrt{9}$,$\sqrt{n+1}-\sqrt{n}$.
点评 本题考查分母有理化,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 如图,等腰△ABC中,AB=AC=13,BC=10,D是BC边上任意一点,DE⊥AB于E,DF⊥AC于点F,则DE+DF=$\frac{120}{13}$.
如图,等腰△ABC中,AB=AC=13,BC=10,D是BC边上任意一点,DE⊥AB于E,DF⊥AC于点F,则DE+DF=$\frac{120}{13}$.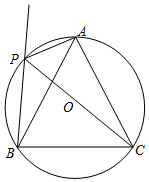 如图,⊙O是等边三角形ABC的外接圆,点P是$\widehat{AB}$上一点,连接AP,CP,作射线BP.
如图,⊙O是等边三角形ABC的外接圆,点P是$\widehat{AB}$上一点,连接AP,CP,作射线BP.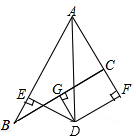 已知:如图∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
已知:如图∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.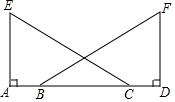 已知:如图,点A,B,C,D同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.问:∠ACE=∠DBF吗?说明理由.
已知:如图,点A,B,C,D同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.问:∠ACE=∠DBF吗?说明理由.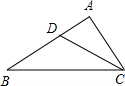 如图,∠ACD=∠B,AC=6,AD=4,则AB=9.
如图,∠ACD=∠B,AC=6,AD=4,则AB=9.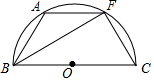 如图,已知BC是⊙O的直径,$\widehat{AB}$=$\widehat{AF}$=$\widehat{FC}$,AF=6,求BF的长.
如图,已知BC是⊙O的直径,$\widehat{AB}$=$\widehat{AF}$=$\widehat{FC}$,AF=6,求BF的长.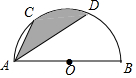 如图,AB为半圆O的直径,C,D为半圆弧的三等分点,若AB=12,则阴影部分的面积为6π.
如图,AB为半圆O的直径,C,D为半圆弧的三等分点,若AB=12,则阴影部分的面积为6π.