题目内容
16. 如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,
如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,(1)若EF=5,BC=16,求△EFM的周长;
(2)若∠ABC=50°,∠ACB=60°,求∠MFE度数.
分析 (1)根据直角三角形的性质得到FM=EM=$\frac{1}{2}$BC=8,于是得到结论;
(2)根据等腰三角形的性质得到∠FMB+∠EMC=140°,根据平角的定义和三角形的内角和得到结论.
解答 解:(1)∵CF⊥AB于F,BE⊥AC于E,
∴∠BFC=∠BEC=90°,
∵M为BC的中点,
∴FM=EM=$\frac{1}{2}$BC=8,
∵EF=5,
∴△EFM的周长=16=5=21;
(2)∵BM=FM,CM=EM,
∴∠BFM=∠ABC=50°,∠EMEC=∠ACB=60°,
∴∠FMB+∠EMC=140°,
∴∠MFE+∠MEF=140°,
∴∠MFE=70°.
点评 本题考查了直角三角形的性质,等腰三角形的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
相关题目
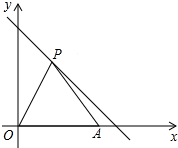 如图,点A坐标为(4,0),点P在第一象限且在直线y=-x+5上.
如图,点A坐标为(4,0),点P在第一象限且在直线y=-x+5上.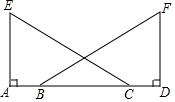 已知:如图,点A,B,C,D同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.问:∠ACE=∠DBF吗?说明理由.
已知:如图,点A,B,C,D同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.问:∠ACE=∠DBF吗?说明理由.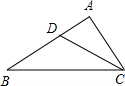 如图,∠ACD=∠B,AC=6,AD=4,则AB=9.
如图,∠ACD=∠B,AC=6,AD=4,则AB=9.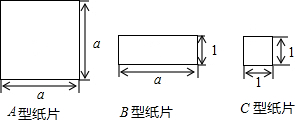
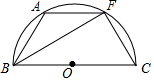 如图,已知BC是⊙O的直径,$\widehat{AB}$=$\widehat{AF}$=$\widehat{FC}$,AF=6,求BF的长.
如图,已知BC是⊙O的直径,$\widehat{AB}$=$\widehat{AF}$=$\widehat{FC}$,AF=6,求BF的长. 结合如下面积为3的正方形,在数轴上表示±$\sqrt{3}$.
结合如下面积为3的正方形,在数轴上表示±$\sqrt{3}$.