题目内容
几何模型
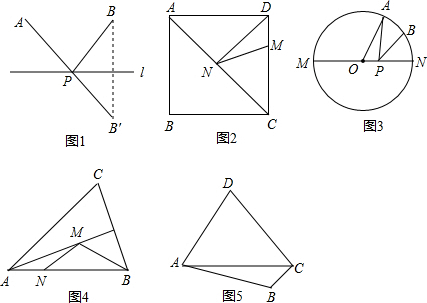
条件:如图1,A、B是直线l同侧的两个定点.
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点B关于直线l的对称点B’,连结AB’交l于点P,则PA+PB=AB’的值最小(不必证明).
直接应用
如图2,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为 .
变式练习
如图3,点A是半圆上(半径为1)的三等分点,B是(
)的中点,P是直径MN上一动点,求PA+PB的最小值.
深化拓展
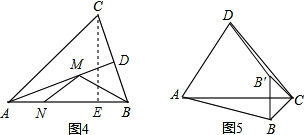
(1)如图4,在锐角△ABC中,AB=4
,∠BAC=45°,∠BAC的平分线交BC 于点D,M、N分别是AD和AB上的动点,求BM+MN的最小值.
(2)如图5,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.
(要求:保留作图痕迹,并简述作法.)
条件:如图1,A、B是直线l同侧的两个定点.
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点B关于直线l的对称点B’,连结AB’交l于点P,则PA+PB=AB’的值最小(不必证明).
直接应用
如图2,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为
变式练习
如图3,点A是半圆上(半径为1)的三等分点,B是(
 |
| AN |
深化拓展
(1)如图4,在锐角△ABC中,AB=4
| 2 |
(2)如图5,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.
(要求:保留作图痕迹,并简述作法.)

考点:几何变换综合题
专题:
分析:直接应用,如图2,连接BM,则BM的长就是DN+NM的最小值,利用勾股定理即可求解;
变式练习:如图3,作B关于MN的对称点C,则C在圆上,且∠AOC=90°,连接AC,则AC的长就是AP+BP的最小值;
(1)作出B关于AM的对称点C,作CE⊥AB于点E,CE的长就是BM+MN的最小值,利用三角函数即可求解;
(2)作点B关于直线AC的对称点B',连接DB'交AC于点P,即为所求.
变式练习:如图3,作B关于MN的对称点C,则C在圆上,且∠AOC=90°,连接AC,则AC的长就是AP+BP的最小值;
(1)作出B关于AM的对称点C,作CE⊥AB于点E,CE的长就是BM+MN的最小值,利用三角函数即可求解;
(2)作点B关于直线AC的对称点B',连接DB'交AC于点P,即为所求.
解答: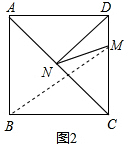 解:直接应用,如图2,连接BM,则BM的长就是DN+NM的最小值.
解:直接应用,如图2,连接BM,则BM的长就是DN+NM的最小值.
在直角△BCM中,BC=8,CM=8-2=6,
则BM=
=
=10;
变式练习:如图3,作B关于MN的对称点C,则C在圆上,且∠AOC=90°,
连接AC,则AC的长就是AP+BP的最小值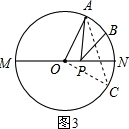 .
.
△AOC是等腰直角三角形,则AC=
OA=
,
即AP+BP的最小值是
;
深化拓展:(1)图4.作出B关于AM的对称点C,作CE⊥AB于点E.
则AC=AB=4
,
CE的长就是BM+MN的最小值,
∵∠BAC=45°,
∴△ACE是等腰直角三角形,
∴CE=
AC=
×4
=4;
(2)作点B关于直线AC的对称点B',连接DB'交AC于点P,即为所求.
 解:直接应用,如图2,连接BM,则BM的长就是DN+NM的最小值.
解:直接应用,如图2,连接BM,则BM的长就是DN+NM的最小值.在直角△BCM中,BC=8,CM=8-2=6,
则BM=
| BC2+CM2 |
| 82+62 |
变式练习:如图3,作B关于MN的对称点C,则C在圆上,且∠AOC=90°,
连接AC,则AC的长就是AP+BP的最小值
 .
.△AOC是等腰直角三角形,则AC=
| 2 |
| 2 |
即AP+BP的最小值是
| 2 |
深化拓展:(1)图4.作出B关于AM的对称点C,作CE⊥AB于点E.
则AC=AB=4
| 2 |
CE的长就是BM+MN的最小值,
∵∠BAC=45°,
∴△ACE是等腰直角三角形,
∴CE=
| ||
| 2 |
| ||
| 2 |
| 2 |
(2)作点B关于直线AC的对称点B',连接DB'交AC于点P,即为所求.

点评:本题考查了轴对称的性质,以及勾股定理和正方形的性质的综合应用,正确确定量线段的长度的最小值是本题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 如图,在边长为4的正方形内部,以各边为直径画四个半圆,则图中阴影部分的面积是( )
如图,在边长为4的正方形内部,以各边为直径画四个半圆,则图中阴影部分的面积是( )| A、4 | B、4π | C、2π-4 | D、2π |
 已知,在如图四边形ABCD中,AB∥CD,AB=CD,点A,B,C在⊙O上,AD是⊙O切线,射线AO交BC于点E,交⊙O于点F.点P在射线AO上,
已知,在如图四边形ABCD中,AB∥CD,AB=CD,点A,B,C在⊙O上,AD是⊙O切线,射线AO交BC于点E,交⊙O于点F.点P在射线AO上,
 如图,图中内错角有
如图,图中内错角有 如图,量角器的直径与含30°角的直角三角形ABC的斜边AB重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,当第30秒时,点E在量角器上对应的读数是( )
如图,量角器的直径与含30°角的直角三角形ABC的斜边AB重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,当第30秒时,点E在量角器上对应的读数是( )