题目内容
 如图,量角器的直径与含30°角的直角三角形ABC的斜边AB重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,当第30秒时,点E在量角器上对应的读数是( )
如图,量角器的直径与含30°角的直角三角形ABC的斜边AB重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,当第30秒时,点E在量角器上对应的读数是( )| A、120° | B、150° |
| C、75° | D、60° |
考点:圆周角定理
专题:
分析:首先连接OE,由∠ACB=90°,根据圆周角定理,可得点C在⊙O上,即可得∠EOA=2∠ECA,又由∠ECA的度数,继而求得答案.
解答: 解:连接OE,
解:连接OE,
∵∠ACB=90°,
∴点C在以AB为直径的圆上,
即点C在⊙O上,
∴∠EOA=2∠ECA,
∵∠ECA=2×30°=60°,
∴∠AOE=2∠ECA=2×60°=120°.
故选A.
 解:连接OE,
解:连接OE,∵∠ACB=90°,
∴点C在以AB为直径的圆上,
即点C在⊙O上,
∴∠EOA=2∠ECA,
∵∠ECA=2×30°=60°,
∴∠AOE=2∠ECA=2×60°=120°.
故选A.
点评:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列水平放置的几何体中,主视图不是矩形的为( )
A、 圆柱 |
B、 长方体 |
C、 三棱柱 |
D、 圆锥 |

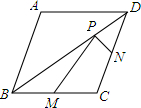 已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上的动点(不含B、D).
已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上的动点(不含B、D).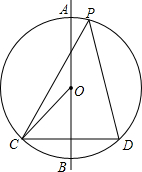 在⊙O中,AB是直径,CD是弦,AB⊥CD.
在⊙O中,AB是直径,CD是弦,AB⊥CD.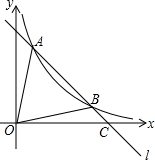 如图,直线l与反比例函数y=
如图,直线l与反比例函数y=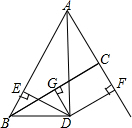 如图,AB>AC,∠BAC的平分线与BC的垂直平分线交于点D,过点D作DE⊥AB于点E,DF⊥AC于点F,∠BDE=∠CDF,BE=3,AC=6,求AE的长.
如图,AB>AC,∠BAC的平分线与BC的垂直平分线交于点D,过点D作DE⊥AB于点E,DF⊥AC于点F,∠BDE=∠CDF,BE=3,AC=6,求AE的长.