题目内容
4. 已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:①当x>0时,y1>y2;②当x<0时,x值越大,M值越大;③使得M大于2的x值不存在;④使得M=1的x值是-$\frac{1}{2}$或$\frac{\sqrt{2}}{2}$.其中正确结论的个数为( )
已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:①当x>0时,y1>y2;②当x<0时,x值越大,M值越大;③使得M大于2的x值不存在;④使得M=1的x值是-$\frac{1}{2}$或$\frac{\sqrt{2}}{2}$.其中正确结论的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 关键函数的增减性,以及M的定义,逐一判断即可.
解答 解:∵x>0时, 函数y2的图象在上面,
函数y2的图象在上面,
∴y2>y1,故①错误.
当x<0时,M的值=y1或y2,
∵x<0,y随x增大而增大,
∴x值越大,M值越大,故②正确.
刚才图象可知M的最大值为2,
∴使得M大于2的x值不存在,故③正确,
y2=1时,x=-$\frac{1}{2}$,
y1=1时,x=±$\frac{\sqrt{2}}{2}$,
观察图象可知:x=-$\frac{1}{2}$或$\frac{\sqrt{2}}{2}$时,M=1,故④正确.
故选D.
点评 本题考查二次函数的性质,解题的关键是理解题意,灵活运用函数的性质解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.使分式$\frac{3}{x-2}$有意义的x的取值范围是( )
| A. | x≠2 | B. | x>2 | C. | x<2 | D. | x≥2 |
19.在下列二次根式:$\sqrt{\frac{1}{3}}$,$\sqrt{2}$+$\sqrt{5}$,$\sqrt{{a}^{2}+{b}^{2}}$,$\sqrt{3ab}$中,是最简二次根式的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.费县为了改善全县中、小学办学条件,计划集中采购一批电子白板和投影机,已知购买2块电子白板比购买3台投影机多4000元,购买4块电子白板和3台投影机共需44000元,则购买一块电子白板和一台投影机分别需要( )
| A. | 4000元,8000元 | B. | 8000元,4000元 | C. | 14000元,8000元 | D. | 10000元,12000元 |
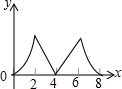
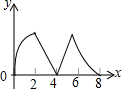
 如图,正方形ABCD边长为4个单位,两动点P、Q分别从点A、B处,以1单位/s、2单位/s的速度逆时针沿边移动.记移动的时间为x(s),△PBQ面积为y(平方单位),当点Q移动一周又回到点B终止,则y与x的函数关系图象为( )
如图,正方形ABCD边长为4个单位,两动点P、Q分别从点A、B处,以1单位/s、2单位/s的速度逆时针沿边移动.记移动的时间为x(s),△PBQ面积为y(平方单位),当点Q移动一周又回到点B终止,则y与x的函数关系图象为( )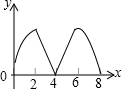

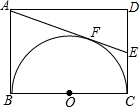 如图所示,在矩形ABCD中,AB=3,BC=4,以BC为直径作半圆O,过点A作半圆O的切线交CD于点E,切点为F,则AE的长为$\frac{13}{3}$.
如图所示,在矩形ABCD中,AB=3,BC=4,以BC为直径作半圆O,过点A作半圆O的切线交CD于点E,切点为F,则AE的长为$\frac{13}{3}$.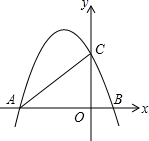 如图,抛物线y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,连接AC、BC.
如图,抛物线y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,连接AC、BC.