题目内容
9.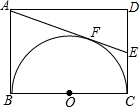 如图所示,在矩形ABCD中,AB=3,BC=4,以BC为直径作半圆O,过点A作半圆O的切线交CD于点E,切点为F,则AE的长为$\frac{13}{3}$.
如图所示,在矩形ABCD中,AB=3,BC=4,以BC为直径作半圆O,过点A作半圆O的切线交CD于点E,切点为F,则AE的长为$\frac{13}{3}$.
分析 易证得AB,CD是⊙O的切线,然后由切线长定理可得AF=AB=3,EF=EC,设AE=x,则EF=AE-AF=x-3,即可得DE=6-x,然后由勾股定理得方程:42+(6-x)2=x2,解此方程即可求得答案.
解答 解:∵四边形ABCD是矩形,
∴∠ABC=∠BCD=90°,CD=AB=3,AD=BC=4,
∴AB,CD是⊙O的切线,
∵AE是⊙O的切线,
∴AF=AB=3,EF=EC,
设AE=x,则EF=AE-AF=x-3,
∴DE=CD-EC=3-(x-3)=6-x,
在Rt△ADE中,AD2+DE2=AE2,
∴42+(6-x)2=x2,
解得:x=$\frac{13}{3}$,
∴AE=$\frac{13}{3}$.
故答案为:$\frac{13}{3}$.
点评 此题考查了切线的性质、切线长定理、矩形的性质以及勾股定理.注意掌握方程思想的应用是解此题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
11.如果a>b,那么下列不等式不成立的是( )
| A. | a-5>b-5 | B. | -5a>-5b | C. | $\frac{a}{2}$>$\frac{b}{2}$ | D. | -0.5a<-0.5b |
14.若直线y=kx+b平行于直线y=3x-4,且过点(1,-2),则该直线的解析式是( )
| A. | y=3x-2 | B. | y=-3x-6 | C. | y=3x-5 | D. | y=3x+5 |
1.根据以下对话,可以求得小红所买的笔和笔记本的价格分别是(


| A. | 3元、2元 | B. | 2元、3元 | C. | 3.4元、1.6元 | D. | 1.6元、3.4元 |

 已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:①当x>0时,y1>y2;②当x<0时,x值越大,M值越大;③使得M大于2的x值不存在;④使得M=1的x值是-$\frac{1}{2}$或$\frac{\sqrt{2}}{2}$.其中正确结论的个数为( )
已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:①当x>0时,y1>y2;②当x<0时,x值越大,M值越大;③使得M大于2的x值不存在;④使得M=1的x值是-$\frac{1}{2}$或$\frac{\sqrt{2}}{2}$.其中正确结论的个数为( )