题目内容
15．
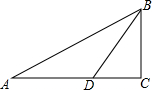如图，在△ABC中，∠C=90°，BD平分∠ABC，BC=3cm，AC=4cm，则△ABD与△BDC的面积之比为5：3．
分析 作DE⊥AB于E，根据角平分线的性质得到DE=DC，根据勾股定理求出AB的长，根据三角形的面积公式计算即可．
解答 解：
作DE⊥AB于E，
∵BD平分∠ABC，∠C=90°，DE⊥AB，
∴DE=DC，
∵∠C=90°，BC=3cm，AC=4cm，
∴AB=5cm，
△ABD与△BDC的面积之比：$\frac{1}{2}$×AB×DE：$\frac{1}{2}$×BC×CD=AB：BC=5：3．
故答案为：5：3．
点评 本题考查的是角平分线的性质，角的平分线上的点到角的两边的距离相等．
练习册系列答案
教材全解字词句篇系列答案
相关题目
5．在△ABC中，A，B都是锐角，且sinA=$\frac{\sqrt{3}}{2}$，tanB=$\sqrt{3}$，AB=8，则AB边上的高为（ ）
| A． | 4$\sqrt{3}$ | B． | 8$\sqrt{3}$ | C． | 16$\sqrt{3}$ | D． | 24$\sqrt{3}$ |
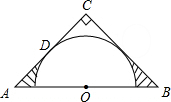如图，在△ABC中，∠C=90°，AC=BC，AB=2$\sqrt{2}$，点O为AB的中点，以点O为圆心作半圆与边AC相切于点D．则图中阴影部分的面积为1-$\frac{π}{4}$．
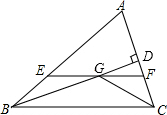如图，在△ABC中，∠ABC和∠ACB的平分线相交于点G，过点G作EF∥BC交AB于E，交AC于F，过点G作GD⊥AC于D，下列四个结论：