题目内容
6.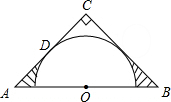 如图,在△ABC中,∠C=90°,AC=BC,AB=2$\sqrt{2}$,点O为AB的中点,以点O为圆心作半圆与边AC相切于点D.则图中阴影部分的面积为1-$\frac{π}{4}$.
如图,在△ABC中,∠C=90°,AC=BC,AB=2$\sqrt{2}$,点O为AB的中点,以点O为圆心作半圆与边AC相切于点D.则图中阴影部分的面积为1-$\frac{π}{4}$.
分析 遇切线,想直角;根据切线,可得∠ADO=90°,根据AB的长,求出AO的长度;解直角三角形,求出半径OD的长度;根据阴影部分的面积=2×(三角形的面积减扇形的面积),计算即可.
解答 解:如右图,连接OD,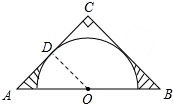
∵AC与⊙O相切,${S}_{阴影}=2(\frac{1}{2}×1×1-\frac{45π×{1}^{2}}{360})=2(\frac{1}{2}-\frac{π}{8})=1-\frac{π}{4}$
∴∠ADO=90°,
∵∠C=90°,CA=CB,
∴∠A=∠B=45°,
∴∠AOD=45°,
∵O是AB的中点,AB=$2\sqrt{2}$,
∴OA=$\sqrt{2}$,
在Rt△AOD中,∠A=45°,OA=$\sqrt{2}$,
∴OD=cos45°•OA=$\frac{\sqrt{2}}{2}×\sqrt{2}$=1,
∴${S}_{阴影}=2(\frac{1}{2}×1×1-\frac{45π×{1}^{2}}{360})=2(\frac{1}{2}-\frac{π}{8})=1-\frac{π}{4}$.
故答案为:1-$\frac{π}{4}$.
点评 本题是切线的性质、等腰三角形的性质、解直角三角形、三角形的面积、扇形的面积的综合应用,根据已知条件求出圆的半径是解决此题的关键.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
17.下列因式分解正确的是( )
| A. | 4a2-4a+1=4a(a-1)+1 | B. | x2-4y2=(x+4y)(x-4y) | ||
| C. | $\frac{9}{4}$x2-x+$\frac{1}{9}$=($\frac{3}{2}$x-$\frac{1}{3}$)2 | D. | 2xy-x2-y2=-(x+y)2 |
14.如果a是b的近似值,那么我们把b叫做a的真值,若用四舍五入法得到的近似数是75,则下列各数不可能是其真值的是( )
| A. | 75.01 | B. | 75.49 | C. | 74.99 | D. | 74.49 |
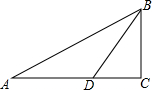 如图,在△ABC中,∠C=90°,BD平分∠ABC,BC=3cm,AC=4cm,则△ABD与△BDC的面积之比为5:3.
如图,在△ABC中,∠C=90°,BD平分∠ABC,BC=3cm,AC=4cm,则△ABD与△BDC的面积之比为5:3. 如图,是在一个直角三角尺中去掉一半径为r的圆,则阴影部分面积为$\frac{1}{2}$ab-πr2.
如图,是在一个直角三角尺中去掉一半径为r的圆,则阴影部分面积为$\frac{1}{2}$ab-πr2.