题目内容
10.已知,一次函数y=-$\frac{1}{2}$x+5与y=2x的图象分别为直线l1和l2,l1与l2交于点A,l1与x轴、y轴交于B、C.(1)求点A的坐标;
(2)求证:l1⊥l2;
(3)平面上有一点M,使得四边形OABM为矩形,求点M坐标.
分析 (1)联立两个一次函数解析式组成方程组,求出方程组的解即可确定出A的坐标;
(2)根据A,O以及B的坐标,求出AO,AB以及OB的长,利用勾股定理的逆定理判断即可;
(3)若四边形OABM为矩形,则有两组对边平行,分别确定出BM与OM所在直线的解析式,联立即可求出M的坐标.
解答  解:(1)联立得:$\left\{\begin{array}{l}{y=-\frac{1}{2}x+5}\\{y=2x}\end{array}\right.$,
解:(1)联立得:$\left\{\begin{array}{l}{y=-\frac{1}{2}x+5}\\{y=2x}\end{array}\right.$,
消去y得:-$\frac{1}{2}$x+5=2x,
解得:x=2,
把x=2代入得:y=4,
则A(2,4);
(2)∵A(2,4),0(0,0),B(10,0),
∴AO=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,AB=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,OB=10,
∴AO2+AB2=OB2,
∴AO⊥AB,即l1⊥l2;
(3)如图所示,若四边形OABM为矩形,则有OA∥BM,AB∥OM,
∴BM所在直线解析式为y=2(x-10)=2x-20,OM所在直线解析式为y=-$\frac{1}{2}$x,
联立得:$\left\{\begin{array}{l}{y=2x-20}\\{y=-\frac{1}{2}x}\end{array}\right.$,
消去y得:2x-20=-$\frac{1}{2}$x,
解得:x=8,
把x=8代入得:y=-4,
则M坐标为(8,-4).
点评 此题属于一次函数综合题,涉及的知识有:两直线交点的求法,两直线垂直时斜率满足的关系,坐标与图形性质,以及矩形的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.用数轴上的点表示有理数,下列说法中不正确的是( )
| A. | 两个有理数,绝对值大的离原点远 | B. | 两个有理数,大的在右边 | ||
| C. | 两个负有理数,大的离原点远 | D. | 两个负有理数,大的离原点近 |
5.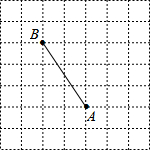 在7×7的方格中,每个小方格的边长均为1,A、B两点都在格点上,若在格点上找到一点P,使△PAB的面积为6,则符合条件的点P有( )
在7×7的方格中,每个小方格的边长均为1,A、B两点都在格点上,若在格点上找到一点P,使△PAB的面积为6,则符合条件的点P有( )
 在7×7的方格中,每个小方格的边长均为1,A、B两点都在格点上,若在格点上找到一点P,使△PAB的面积为6,则符合条件的点P有( )
在7×7的方格中,每个小方格的边长均为1,A、B两点都在格点上,若在格点上找到一点P,使△PAB的面积为6,则符合条件的点P有( )| A. | 2个 | B. | 4个 | C. | 8个 | D. | 12个 |
 如图,在平面直角坐标中,A点坐标为(0,4),B点坐标为(3,0),OD⊥AB于点D,试求D点的坐标.
如图,在平面直角坐标中,A点坐标为(0,4),B点坐标为(3,0),OD⊥AB于点D,试求D点的坐标. 甲、乙两车同时以一定的速度从A城出发前往B城,行驶途中甲接到电话,立刻以同样的速度返回A城,然后提高速度前往B城,结果比乙车早到1小时,设甲、乙两车从A城出发的时间为t(小时),距离A城距离为y km,如图所示,则A,B两城距离是300km.
甲、乙两车同时以一定的速度从A城出发前往B城,行驶途中甲接到电话,立刻以同样的速度返回A城,然后提高速度前往B城,结果比乙车早到1小时,设甲、乙两车从A城出发的时间为t(小时),距离A城距离为y km,如图所示,则A,B两城距离是300km. 在梯形ABCD中,AD∥BC,点E、F分别在边AB、CD上.EF∥BC,EF交AC于G.EB=DF,AE=9,CF=4.求BE,CD,$\frac{GF}{AD}$的值.
在梯形ABCD中,AD∥BC,点E、F分别在边AB、CD上.EF∥BC,EF交AC于G.EB=DF,AE=9,CF=4.求BE,CD,$\frac{GF}{AD}$的值. 如图,在△ABC中,AD平分∠BAC,过D作DE∥AC交AB于E,过E作AD的垂线交AD于O,交BC的延长线于F,连接AF,求证:∠CAF=∠B.
如图,在△ABC中,AD平分∠BAC,过D作DE∥AC交AB于E,过E作AD的垂线交AD于O,交BC的延长线于F,连接AF,求证:∠CAF=∠B.