题目内容
7.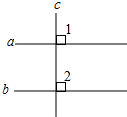 如图,已知a∥b,如果c⊥a,判断c与b的位置关系,并说明理由.
如图,已知a∥b,如果c⊥a,判断c与b的位置关系,并说明理由.∵a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等),
∵c⊥a(已知),
∴∠1=90°(垂直的性质),
∴∠2=90°(等量代换),
∴c⊥b(垂直的定义)
分析 根据平行线的性质“两直线平行,同位角相等”得出∠1=∠2,再根据垂线的定义和性质即可得出结论.
解答 证明:a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等),
∵c⊥a(已知),
∴∠1=90°(垂直的性质),
∴∠2=90°(等量代换),
∴c⊥b(垂直的定义).
故答案为:∠2;两直线平行,同位角相等;90°;垂直的性质;90°;等量代换;垂直的定义.
点评 本题考查了平行线的性质和垂直的定义及性质,解题的关键是利用“两直线平行,同位角相等”得出结论.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质找出相等(或互补)的角是关键.

练习册系列答案
相关题目
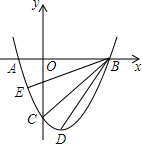 如图,抛物线y=ax2-2ax+b与x轴交于A、B两点,交y轴负半轴于点C,已知B(3,0),C(0,-3),D为顶点.
如图,抛物线y=ax2-2ax+b与x轴交于A、B两点,交y轴负半轴于点C,已知B(3,0),C(0,-3),D为顶点.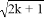 x+1=0有两个不相等的实数根,那么k的取值范围是( )
x+1=0有两个不相等的实数根,那么k的取值范围是( ) B. k<
B. k<