题目内容
1.如图,点D是等边△ABC的边AB上一点,连接CD并以CD为边等边△CDE,连接BE(1)求证:AD=BE;
(2)过点D作DF⊥BC于点F,连接AF,AF∥DE,AB=3,求线段CF的长度.
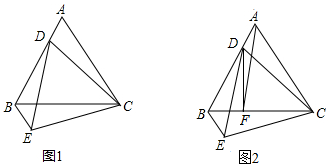
分析 (1)根据等边三角形的性质得到AC=BC,DC=EC,∠ACB=∠DCE=60°,推出△ACD≌△BCE,根据求三角形的性质得到AD=BE;
(2)根据平行线的性质得到∠BAF=∠BDE,推出∠BAF=∠BDE=∠ACD=∠BCE,证得△ABF≌△CBE,由全等三角形的性质得到BF=BE解直角三角形即可得到结论.
解答 (1)证明:∵△ABC,△CDE是等边三角形,
∴AC=BC,DC=EC,∠ACB=∠DCE=60°,
∴∠ACD=60°-∠BCD=∠BCE,
在△ACD与△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{DC=EC}\end{array}\right.$,
∴△ACD≌△BCE,
∴AD=BE;
(2)解:∵AF∥DE,
∴∠BAF=∠BDE,
∵∠BDC=∠BDE+CDE=∠BDE+60°=∠BAC+∠ACD,
∴∠BAF=∠BDE=∠ACD=∠BCE,
在△ABF与△CBE中,
$\left\{\begin{array}{l}{∠BAF=∠BCE}\\{AB=BC}\\{∠ABF=∠CBE}\end{array}\right.$,
∴△ABF≌△CBE,
∴BF=BE,
∵DF⊥BC,∠ABC=60°,
∴AD=BE=BF=BD•cos∠ABC=$\frac{1}{2}$BD,
∵AB=BC,AD=BF,
∴CF=BD=2BF,
∴CF=$\frac{2}{3}$BC=$\frac{2}{3}$AB=$\frac{2}{3}$×3=2.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质,平行线的性质,解直角三角形,熟练掌握全等三角形的性质是解题的关键.

练习册系列答案
相关题目
 D. 4
D. 4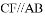 ,交DE的延长线于点F.求证:AD = CF.
,交DE的延长线于点F.求证:AD = CF.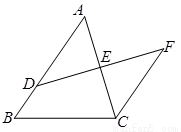
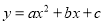 经过点A(5,0),B(-3,0),C(0,4).
经过点A(5,0),B(-3,0),C(0,4). 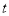 (秒)(0<
(秒)(0<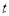 <7),△PQB的面积记为S.
<7),△PQB的面积记为S.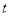 的函数关系式;
的函数关系式;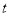 为何值时,S有最大值,最大值是多少?
为何值时,S有最大值,最大值是多少?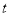 值,使得△PQB是直角三角形?若存在,请直接写出
值,使得△PQB是直角三角形?若存在,请直接写出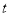 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.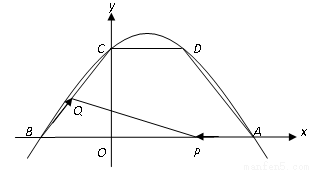
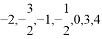 这七个数中,随机取出一个数,记为
这七个数中,随机取出一个数,记为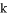 ,那么
,那么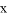 的函数
的函数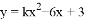 与
与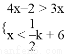 有且只有3个整数解的概率为___________ .
有且只有3个整数解的概率为___________ .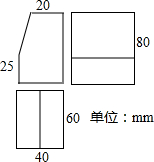 已知一个几何体的三视图如图所示.
已知一个几何体的三视图如图所示.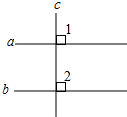 如图,已知a∥b,如果c⊥a,判断c与b的位置关系,并说明理由.
如图,已知a∥b,如果c⊥a,判断c与b的位置关系,并说明理由.