题目内容
19.已知抛物线y=x2+mx-$\frac{3}{4}$m2与x轴交于A(x1,0)、B(x2,0)两点,x1<0<x2,且A、B两点到原点的距离AO、BO满足$\frac{1}{BO}$-$\frac{1}{AO}$=$\frac{2}{3}$,则这个函数的解析式为y=x2+2x-3.分析 由题意可知x1、x2是方程x2+mx-$\frac{3}{4}$=0的两个实数根,根据一元二次方程根与系数的关系及已知条件,可求出m的值,进而得到抛物线的解析式.
解答 解:
∵抛物线y=x2+mx-$\frac{3}{4}$m2与x轴交于A(x1,0)、B(x2,0)两点,
∴x1、x2是方程x2+mx-$\frac{3}{4}$=0的两个实数根,
∴x1+x2=-m,x1•x2=-$\frac{3}{4}$m2,
∵AO=-x1,OB=x2,
∵$\frac{1}{BO}$-$\frac{1}{AO}$=$\frac{2}{3}$,
∴$\frac{1}{{x}_{2}}-\frac{1}{{-x}_{1}}$=$\frac{2}{3}$,
∴$\frac{{x}_{1}{+x}_{2}}{{x}_{1}•{x}_{2}}$=$\frac{2}{3}$,
∴$\frac{-m}{-\frac{3}{4}{m}^{2}}$=$\frac{2}{3}$,
解得m=2,经检验,m=2是方程的解.
∴所求抛物线的解析式为y=x2+2x-3,
故答案为:y=x2+2x-3.
点评 本题考查了抛物线与x轴的交点坐标的求法、解方程等知识;熟练掌握抛物线与x轴的交点特征,求出抛物线与x轴的交点坐标是解决问题的关键.

练习册系列答案
相关题目
4.求一个数的立方根,有些数可以直接求得,如$\root{3}{8}$,有些数则不能直接求得,如$\root{3}{5}$,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
(1)表中所给的信息中,你能发现什么规律?(请将规律用文字表达出来)
(2)运用你发现的规律,探究下列问题:
已知$\root{3}{2.5}$≈1.36,求下列各数的立方根:
①0.0025; ②2500000.
| n | 8 | 0.008 | 0.000008 | 8000 | 8000000 | … |
| $\root{3}{n}$ | 2 | 0.2 | 0.02 | 20 | 200 | … |
(2)运用你发现的规律,探究下列问题:
已知$\root{3}{2.5}$≈1.36,求下列各数的立方根:
①0.0025; ②2500000.
6.一元一次不等式2x+1≥0的解集是( )
| A. | x≥$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$ | C. | x≥-$\frac{1}{2}$ | D. | x≤-$\frac{1}{2}$ |
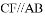 ,交DE的延长线于点F.求证:AD = CF.
,交DE的延长线于点F.求证:AD = CF.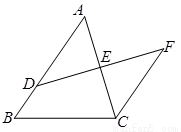
 已知一个几何体的三视图如图所示.
已知一个几何体的三视图如图所示.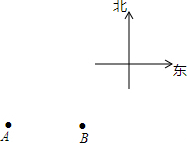 如图,A点和B点表示地面上的两个观测点,从A点观测到它的北偏东30°方向有一个读书亭C,同时,从B点观测到这个读书亭C在它的北偏西45°方向,试在图中确定读书亭C的位置.
如图,A点和B点表示地面上的两个观测点,从A点观测到它的北偏东30°方向有一个读书亭C,同时,从B点观测到这个读书亭C在它的北偏西45°方向,试在图中确定读书亭C的位置.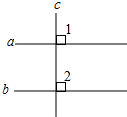 如图,已知a∥b,如果c⊥a,判断c与b的位置关系,并说明理由.
如图,已知a∥b,如果c⊥a,判断c与b的位置关系,并说明理由.