题目内容
 已知,△ABC中,AB=AC,在AB上取一点D,在AC延长线上取一点E,连接DE交BC于点F.若F是DE中点,求证:BD=CE.
已知,△ABC中,AB=AC,在AB上取一点D,在AC延长线上取一点E,连接DE交BC于点F.若F是DE中点,求证:BD=CE.考点:全等三角形的判定与性质,等腰三角形的性质
专题:证明题
分析:过点D作DP∥AC交BC于P,就可以得出∠DPB=∠ACB,△DPF≌△ECF,就可以得出DP=EC,由BD=DP就可以得出结论.
解答: 证明:过点D作DP∥AC交BC于P,
证明:过点D作DP∥AC交BC于P,
∴∠DPB=∠ACB,∠DPF=∠ECF.
∵F是DE中点,
∴DF=EF.
在△DPF和△ECF中
,
∴△DPF≌△ECF(AAS),
∴DP=EC.
∵AB=AC,
∴∠ABC=∠ACB,
∴∠DPB=∠ABC,
∴BD=DP,
∴BD=EC.
 证明:过点D作DP∥AC交BC于P,
证明:过点D作DP∥AC交BC于P,∴∠DPB=∠ACB,∠DPF=∠ECF.
∵F是DE中点,
∴DF=EF.
在△DPF和△ECF中
|
∴△DPF≌△ECF(AAS),
∴DP=EC.
∵AB=AC,
∴∠ABC=∠ACB,
∴∠DPB=∠ABC,
∴BD=DP,
∴BD=EC.
点评:本题考查了等腰三角形的性质的运用,平行线的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
四边形的四边依次为a,b,c,d,且满足a2+b2+c2+d2-ab-bc-ad-cd=0,则四边形是( )
| A、平行四边形 | B、矩形 |
| C、菱形 | D、正方形 |
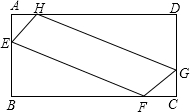 为了美化校园环境,某校准备在一块空地(如图所示的长方形ABCD,AB=10m,BC=20m)上进行绿化,中间的一块(图中四边形EFGH)上种花,其他的四块(图中的四个直角三角形)上铺设草坪,并要求AE=AH=CF=CG,那么在满足上述条件的所有设计中,是否存在一种设计,使得四边形EFGH的面积最大?
为了美化校园环境,某校准备在一块空地(如图所示的长方形ABCD,AB=10m,BC=20m)上进行绿化,中间的一块(图中四边形EFGH)上种花,其他的四块(图中的四个直角三角形)上铺设草坪,并要求AE=AH=CF=CG,那么在满足上述条件的所有设计中,是否存在一种设计,使得四边形EFGH的面积最大? 如图,已知反比例函数
如图,已知反比例函数 如图,已知O为坐标原点,将直线y=x向右平移2个单位后与双曲线y=
如图,已知O为坐标原点,将直线y=x向右平移2个单位后与双曲线y=