题目内容
已知抛物线y=x2-2013x+2014与x轴的交点为(m,0),(n,0),则(m2-2013m+2014)+(n2-2013n+2014)的值是( )
| A、0 | B、2013 |
| C、2014 | D、2015 |
考点:抛物线与x轴的交点
专题:
分析:由题意函数y=x2-2013x+2014与x轴的交点为(m,0),(n,0),得到方程m2-2013m+2014=0,n2-2013n+2014=0,然后再代入求得数值即可.
解答:解:∵抛物线y=x2-2013x+2014与x轴的交点为(m,0),(n,0),
∴m2-2013m+2014=0,n2-2013n+2014=0,
∴(m2-2013m+2014)+(n2-2013n+2014)=0.
故选:A.
∴m2-2013m+2014=0,n2-2013n+2014=0,
∴(m2-2013m+2014)+(n2-2013n+2014)=0.
故选:A.
点评:本题考查了抛物线与x轴的交点,揭示了二次函数与一元二次方程间的联系,应用了方程的根的定义.

练习册系列答案
相关题目
在?ABCD中,AB=20,AD=16,AB和CD之间的距离为8,则AD与BC之间的距离为( )
| A、8 | B、9 | C、10 | D、11 |
若多项式(x+2y)2-6x(x+2y)有一个因式为x+2y,则另一个因式为( )
| A、2x-5y |
| B、-5x-2y |
| C、-5x+2y |
| D、5x+2y |
当一个圆锥的底面半径变为原来的2倍,高变为原来的
时,它的体积变为原来的( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
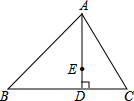 如图,△ABC的底边边长BC=a,当顶点A沿BC边上的高AD向点D移动到点E,使DE=
如图,△ABC的底边边长BC=a,当顶点A沿BC边上的高AD向点D移动到点E,使DE=| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
四边形的四边依次为a,b,c,d,且满足a2+b2+c2+d2-ab-bc-ad-cd=0,则四边形是( )
| A、平行四边形 | B、矩形 |
| C、菱形 | D、正方形 |
下列各式中,正确的是( )
A、已知ab>0,则
| ||||||||||||||||
B、2
| ||||||||||||||||
C、
| ||||||||||||||||
D、
|