题目内容
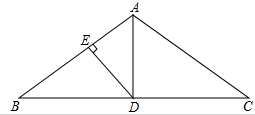 如图所示,在△ABC中,∠BAC=120°,AB=AC,AD是高,DE⊥AB于点E,且AE=2,求AB的长.
如图所示,在△ABC中,∠BAC=120°,AB=AC,AD是高,DE⊥AB于点E,且AE=2,求AB的长.考点:含30度角的直角三角形,等腰三角形的性质
专题:
分析:根据题意知AD⊥BC,从而可利用直角三角形中30度的角所对的边是斜边的一半求得AD的长,同理可求得AE的长,再在直角△ABD中求AB的长度.
解答: 解:如图,∵在△ABC中,∠BAC=120°,AB=AC,AD是高,
解:如图,∵在△ABC中,∠BAC=120°,AB=AC,AD是高,
∴∠BAD=∠CAD=
∠BAC=60°,
∴∠B=30°,
∴AB=2AD.
又∵DE⊥AB,
∴∠EDA=∠30°,
∴AD=2AE.
∴AB=4AE.
又∵AE=2,
∴AB=8.
 解:如图,∵在△ABC中,∠BAC=120°,AB=AC,AD是高,
解:如图,∵在△ABC中,∠BAC=120°,AB=AC,AD是高,∴∠BAD=∠CAD=
| 1 |
| 2 |
∴∠B=30°,
∴AB=2AD.
又∵DE⊥AB,
∴∠EDA=∠30°,
∴AD=2AE.
∴AB=4AE.
又∵AE=2,
∴AB=8.
点评:本题考查了等腰三角形的性质和含30度角的直角三角形的性质,要熟练掌握好边角之间的关系.

练习册系列答案
相关题目
已知一次函数y=kx+b(k≠0)经过(3,-1)、(-6,5)两点,则它的图象不经过( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 一个零件的形状如图所示,按规定∠BAC=90°,∠B=21°,∠C=20°,测量工人量得∠BDC=130°,就判定这个零件不合格,你能运用所学的知识说出其中的道理么?
一个零件的形状如图所示,按规定∠BAC=90°,∠B=21°,∠C=20°,测量工人量得∠BDC=130°,就判定这个零件不合格,你能运用所学的知识说出其中的道理么?