题目内容
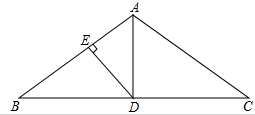
一个零件的形状如图所示，按规定∠BAC=90°，∠B=21°，∠C=20°，测量工人量得∠BDC=130°，就判定这个零件不合格，你能运用所学的知识说出其中的道理么？考点：三角形的外角性质
专题：应用题
分析：延长CD交AB于E，根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠BDC，然后即可判断．
解答：
解：这个零件不合格．
理由：如图，延长CD交AB于E，
∵∠A=90°，∠C=20°，
∴∠1=∠A+∠C=90°+20°=110°，
∵∠B=21°，
∴∠BDC=∠B+∠1=21°+110°=131°．
又∵测量工人量得∠BDC=130°，
∴这个零件不合格．
解：这个零件不合格．理由：如图，延长CD交AB于E，
∵∠A=90°，∠C=20°，
∴∠1=∠A+∠C=90°+20°=110°，
∵∠B=21°，
∴∠BDC=∠B+∠1=21°+110°=131°．
又∵测量工人量得∠BDC=130°，
∴这个零件不合格．
点评：本题考查的是三角形外角的性质，熟知三角形的一个外角等于与它不相邻的两个内角的和的性质是解题的关键．
练习册系列答案
相关题目
关于x的一元二次方程（a-1）x2+x+a2-1=0的一个根是0，则a的值为（ ）
| A、-1 | B、1 |
| C、1或-1 | D、0.5 |
平面直角坐标系内，n为有理数时，点（n，3-2n）一定不在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
如图所示，在△ABC中，∠BAC=120°，AB=AC，AD是高，DE⊥AB于点E，且AE=2，求AB的长．
如图所示，直线AB与CD相交于点O，OE平分∠BOD，若∠BOE=30°，则∠AOC=