题目内容
14．
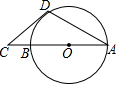如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠C=40°，则∠CDA的度数是（ ）| A． | 110° | B． | 115° | C． | 120° | D． | 125° |
分析 连接OD，如图，根据切线的性质得∠ODC=90°，利用互余得∠COD=50°，再利用等腰三角形的性质和三角形外角性质可得∠ODA=$\frac{1}{2}$∠COD=25°，然后计算∠ODC+∠ODA即可．
解答 解：连接OD，如图，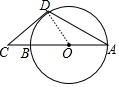
∵CD与⊙O相切于点D，
∴OD⊥CD，
∴∠ODC=90°，
∴∠COD=90°-∠C=90°-40°=50°，
∵OA=OD，
∴∠A=∠ODA，
而∠COD=∠A+∠ODA，
∴∠ODA=$\frac{1}{2}$∠COD=25°，
∴∠CDA=∠ODC+∠ODA=90°+25°=115°．
故选B．
点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．
练习册系列答案
相关题目
4．
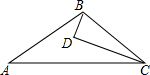如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A=∠ABD，若AC=5，BC=3，则BD的长为（ ）
如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A=∠ABD，若AC=5，BC=3，则BD的长为（ ）| A． | 1 | B． | 1.5 | C． | 2$\sqrt{2}$ | D． | 4 |
5．对于a＞b＞c＞0，m＞n＞0（m、n是正整数），成立的关系式是（ ）
| A． | ambn＞bncm＞cnam | B． | ambn＞cnam＞bncm | C． | amcn＞ambn＞bncm | D． | bnam＞cnam＞ambn |
2．
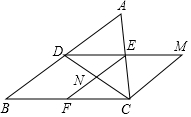如图，在三边互不相等的△ABC中，D、E、F分别是AB、AC、BC边的中点，连接DE，过点C作CM∥AB交DE的延长线于点M，连接CD、EF交于点N，则图中全等三角形共有（ ）
如图，在三边互不相等的△ABC中，D、E、F分别是AB、AC、BC边的中点，连接DE，过点C作CM∥AB交DE的延长线于点M，连接CD、EF交于点N，则图中全等三角形共有（ ）| A． | 3对 | B． | 4对 | C． | 5对 | D． | 6对 |
19．
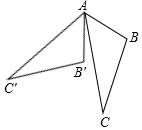如图所示，△ABC中，∠BAC=32°，将△ABC绕点A按顺时针方向旋转55°，对应得到△AB′C′，则∠B′AC的度数为（ ）
如图所示，△ABC中，∠BAC=32°，将△ABC绕点A按顺时针方向旋转55°，对应得到△AB′C′，则∠B′AC的度数为（ ）| A． | 22° | B． | 23° | C． | 24° | D． | 25° |
6．下列运算正确的是（ ）
| A． | x3•x4=x12 | B． | （-6x4）÷（-2x2）=3x3 | C． | （-2a2）2=4a4 | D． | （x-3）2=x2-9 |
