题目内容
4.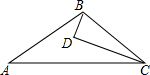 如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )
如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )| A. | 1 | B. | 1.5 | C. | 2$\sqrt{2}$ | D. | 4 |
分析 延长BD与AC交于点E,由题意可推出BE=AE,依据等角的余角相等,即可得等腰三角形BCE,可推出BC=CE,AE=BE=2BD,根据AC=5,BC=3,即可推出BD的长度.
解答 解:延长BD与AC交于点E,
∵∠A=∠ABD,
∴BE=AE,
∵BD⊥CD,
∴BE⊥CD,
∵CD平分∠ACB,
∴∠BCD=∠ECD,
∴∠EBC=∠BEC,
∴△BEC为等腰三角形,
∴BC=CE,
∵BE⊥CD,
∴2BD=BE,
∵AC=5,BC=3,
∴CE=3,
∴AE=AC-EC=5-3=2,
∴BE=2,
∴BD=1.
故选A
点评 本题主要考查等腰三角形的判定与性质,比较简单,关键在于正确地作出辅助线,构建等腰三角形,通过等量代换,即可推出结论.

练习册系列答案
相关题目
14.把分式$\frac{xy}{{x}^{2}+{y}^{2}}$中x,y的值都扩大3倍,所得分式的值( )
| A. | 不变 | B. | 扩大3倍 | C. | 缩小3倍 | D. | 扩大9倍 |
15.抛物线y=(x+1)2+2的顶点是( )
| A. | (1,2) | B. | (-1,2) | C. | (-1,-2) | D. | (1,-2) |
19.下列各组单项式中,不是同类项的一组是( )
| A. | x2y和2xy2 | B. | -32和3 | C. | 3xy和-$\frac{xy}{2}$ | D. | 5x2y和-2yx2 |
9.某班男生有x人,女生人数占全班人数的45%,则该班女生人数是( )人.
| A. | 45%x | B. | 45%+x | C. | $\frac{x}{45%}$-x | D. | $\frac{x}{1-45%}$-x |
16.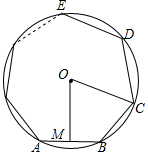 如图,点M是⊙O内接正n边形ABCDE…边AB的中点,连接OM、OC,则∠MOC的度数为( )
如图,点M是⊙O内接正n边形ABCDE…边AB的中点,连接OM、OC,则∠MOC的度数为( )
 如图,点M是⊙O内接正n边形ABCDE…边AB的中点,连接OM、OC,则∠MOC的度数为( )
如图,点M是⊙O内接正n边形ABCDE…边AB的中点,连接OM、OC,则∠MOC的度数为( )| A. | 180°-$\frac{360°}{n}$ | B. | $\frac{360°}{n}$ | C. | $\frac{540°}{n}$ | D. | $\frac{720°}{n}$ |
13.若二次根式$\sqrt{2-x}$有意义,则x的取值范围为( )
| A. | x<2 | B. | x>2 | C. | x≤2 | D. | x≥2 |
14.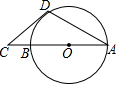 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=40°,则∠CDA的度数是( )
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=40°,则∠CDA的度数是( )
 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=40°,则∠CDA的度数是( )
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=40°,则∠CDA的度数是( )| A. | 110° | B. | 115° | C. | 120° | D. | 125° |