题目内容
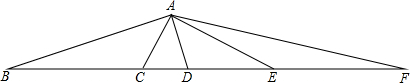
 如图,有两个半径差1的圆,它们各有一个内接正八边形.已知阴影部分的面积是4
如图,有两个半径差1的圆,它们各有一个内接正八边形.已知阴影部分的面积是4| 2 |
A、
| ||
| B、3 | ||
| C、2 | ||
D、
|
考点:正多边形和圆
专题:探究型
分析:连接OB,过点C作CE⊥OB于点E,过点A作AF⊥OB与F,设大圆的半径为r,则小圆的半径为r-1,再用r表示出CE与AF的值,根据阴影部分的面积是4
列出关于r的方程,求出r的值即可.
| 2 |
解答: 解:连接OB,过点C作CE⊥OB于点E,过点A作AF⊥OB与F,设大圆的半径为r,则小圆的半径为r-1,
解:连接OB,过点C作CE⊥OB于点E,过点A作AF⊥OB与F,设大圆的半径为r,则小圆的半径为r-1,
∵两个多边形均是正八边形,
∴∠AOB=45°,
∴AD=OA•sin45°=
,CE=
,
∵阴影部分的面积是4
,
∴S四边形ACDB=
=
,即S△AOB-S△COD=
r•
-
(r-1)•
=
,解得r=
.
故选A.
 解:连接OB,过点C作CE⊥OB于点E,过点A作AF⊥OB与F,设大圆的半径为r,则小圆的半径为r-1,
解:连接OB,过点C作CE⊥OB于点E,过点A作AF⊥OB与F,设大圆的半径为r,则小圆的半径为r-1,∵两个多边形均是正八边形,
∴∠AOB=45°,
∴AD=OA•sin45°=
| ||
| 2 |
| ||
| 2 |
∵阴影部分的面积是4
| 2 |
∴S四边形ACDB=
4
| ||
| 8 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
故选A.
点评:本题考查的是正多边形和圆,解答此题的关键是把阴影部分的面积转化为两三角形面积的差求解.

练习册系列答案
相关题目
若x,y为实数,且|x-2|+(y+1)2=0,则
的值是( )
| x-y |
| A、1 | ||
| B、0 | ||
C、
| ||
D、
|
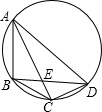 如图,A、B、C、D在同一圆周上,AC与BD交于E,且BC=CD=2,AE=3,则CE的长是
如图,A、B、C、D在同一圆周上,AC与BD交于E,且BC=CD=2,AE=3,则CE的长是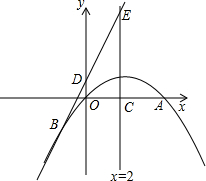 如图,已知二次函数y=ax2+bx+c的图象经过原点O和x轴上的另一点A,它的对称轴直线x=2与x轴交于点C,直线y=2x+1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于D、E.
如图,已知二次函数y=ax2+bx+c的图象经过原点O和x轴上的另一点A,它的对称轴直线x=2与x轴交于点C,直线y=2x+1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于D、E.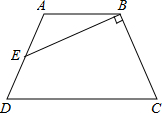 如图,已知等腰梯形ABCD中,AB∥CD,AB=2,CD=4,AD=BC,E是AD的中点,EB⊥BC,则梯形ABCD的面积是
如图,已知等腰梯形ABCD中,AB∥CD,AB=2,CD=4,AD=BC,E是AD的中点,EB⊥BC,则梯形ABCD的面积是