Question

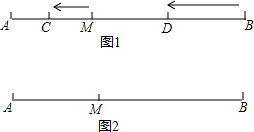
5．已知：如图1，M是定长线段AB上一定点，CD两点分别从M，B出发以1cm/s、4cm/s的速度沿直线BA向左运动．（C在线段AM上，D在线段BM上）
（1）若AB=10cm，当点C、D运动了1s，求AC+MD的值．
（2）若点C、D运动时，总有MD=4AC，直接填空：AM=$\frac{1}{4}$AB．
（3）在（2）的条件下，N是直线AB上一点，且AN-BN=MN，求$\frac{MN}{AB}$的值．

Answer 1

分析 （1）计算出CM及BD的长，进而可得出答案；
（2）根据图形即可直接解答；
（3）分两种情况讨论，①当点N在线段AB上时，②当点N在线段AB的延长线上时，然后根据数量关系即可求解．

解答 解：（1）由题意得，MC=1cm，BD=4cm，
则AC+MD=AB-MC-BD=5cm；
（2）∵BD=4MC，又MD=4AC，
∴AM=$\frac{1}{4}$AB，
故答案为：$\frac{1}{4}$；
（3）当点N在线段AB上时，如图2：
∵AN-BN=MN，
又∵AN-AM=MN
∴BN=AM=$\frac{1}{4}$AB，
∴MN=$\frac{1}{2}$AB，即$\frac{MN}{AB}$=$\frac{1}{2}$；
当点N在线段AB的延长线上时，如图3，
∵AN-BN=MN，又∵AN-BN=AB，
∴MN=AB，即$\frac{MN}{AB}$=1．
综上所述$\frac{MN}{AB}$=$\frac{1}{2}$或1．

点评 本题考查的是两点间的距离的计算，灵活运用数形结合思想是解题的关键．