题目内容
16.某商店经销甲、乙两种商品,现有如下信息:信息1:甲、乙两种商品的进货单价之和是3元;
信息2:甲商品零售单价比进货单价多1元,乙商品零售单价比进货单价的2倍少1元;
信息3:按零售单价购买甲商品3件和乙商品2件,共付了12元.
请根据以上信息,解答下列问题:
(1)求甲、乙两种商品的零售单价;
(2)该商店平均每天卖出甲乙两种商品各500件,经调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件,商店决定把甲种商品的零售单价下降m(m>0)元.在不考虑其他因素的条件下,当m为多少时,商店每天销售甲、乙两种商品获取的总利润为1000元?
分析 (1)根据图上信息可以得出甲乙商品之间价格之间的等量关系,即可得出方程组求出即可;
(2)根据降价后甲每天分别卖出:(500+$\frac{m}{0.1}$×100)件件,每件降价后每件利润分别为:(1-m)元;即可得出总利润,利用方程解答即可.
解答 22.(1)假设甲种商品的进货单价为x元、乙种商品的进货单价为y元,
根据题意可得:$\left\{\begin{array}{l}{x+y=3}\\{3(x+1)+2(2y-1)=12}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
答:甲、乙零售单价分别为2元和3元.
(2)根据题意得出:(1-m)(500+$\frac{m}{0.1}$×100)+500=1000
即2m2-m=0,
解得m=0.5或m=0(舍去),
答:当m定为0.5元才能使商店每天销售甲、乙两种商品获取的利润共1000元.
点评 此题主要考查了二元一次方程的应用,一元二次方程的应用,此题比较典型也是近几年中考中热点题型,注意表示总利润时分别表示出商品的单件利润和所卖商品件数是解决问题的关键.

练习册系列答案
相关题目
8. 如图,将一块三角板的45°顶点放在直尺的一边上,当∠1=63°时,∠2=( )
如图,将一块三角板的45°顶点放在直尺的一边上,当∠1=63°时,∠2=( )
 如图,将一块三角板的45°顶点放在直尺的一边上,当∠1=63°时,∠2=( )
如图,将一块三角板的45°顶点放在直尺的一边上,当∠1=63°时,∠2=( )| A. | 108° | B. | 72° | C. | 77° | D. | 82° |
6. 如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD=( )
如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD=( )
 如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD=( )
如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD=( )| A. | 145° | B. | 150° | C. | 155° | D. | 160° |
 如图,AE∥BF,AC平分∠BAE,交BF于C.
如图,AE∥BF,AC平分∠BAE,交BF于C.
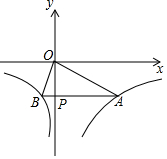 已知函数y=$\left\{\begin{array}{l}-\frac{12}{x}({x>0})\\ \frac{3}{x}({x<0})\end{array}$的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:
已知函数y=$\left\{\begin{array}{l}-\frac{12}{x}({x>0})\\ \frac{3}{x}({x<0})\end{array}$的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论: