题目内容
1.如图,在矩形ABCD中,已知AB=2,BC=3,点E,F,G,H分别在矩形的四条边上,EF与GH交于点O,连结HE,GF.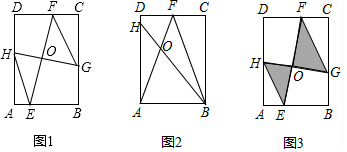
(1)如图1,若HE∥GF,求证:△AEH∽△CFG;
(2)当点E,G分别与点A,B重合时,如图2所示,若点F是CD的中点,且∠AHB=∠AFB,求AH+BH的值;
(3)当GH⊥EF,HE∥FG时,如图3所示,若FO:OE=3:2,且阴影部分的面积等于$\frac{26}{15}$,求EF,HG的长.
分析 (1)在矩形ABCD中,∠A=∠C=90°,只要证明∠AEH=∠CFG即可证明;
(2)如图2中,过点A作AR⊥BF于R.AF=BF=$\sqrt{B{C}^{2}+C{F}^{2}}$=$\sqrt{10}$,由S△ABF=$\frac{1}{2}$•BF•AR=$\frac{1}{2}$×3×2,推出AR=$\frac{3}{5}\sqrt{10}$,RF=$\frac{4}{5}$$\sqrt{10}$,由△BAH∽△ARF,AB:AH:BH=AR:RF:AF=3:4:5,AB=2,可得AH=$\frac{8}{3}$,BH=$\frac{10}{3}$;
(3)如图3中,过F、G分别作FM⊥AB于M,GN⊥AD于N,则△FME∽△GNH,可得$\frac{EF}{GH}$=$\frac{FM}{GN}$=$\frac{3}{2}$,设OF=9x,OE=6x,则GO=6x,OH=4x,由S阴=S△FOG+S△EOH=$\frac{1}{2}$•6x•9x+$\frac{1}{2}$•6x•4x=39x2=$\frac{26}{15}$,解得x=$\frac{\sqrt{10}}{15}$,由此即可解决问题;
解答 解:(1)如图1中,
在矩形ABCD中,∠A=∠C=90°,AB∥CD,
∴∠AEF=∠CFE,
∵HE∥GF,
∴∠HEF=∠GFE,
∴∠AEH=∠CFG,
∴△AEH∽△CFG.
(2)如图2中,过点A作AR⊥BF于R.
∵AF=BF=$\sqrt{B{C}^{2}+C{F}^{2}}$=$\sqrt{10}$,S△ABF=$\frac{1}{2}$•BF•AR=$\frac{1}{2}$×3×2,
∴AR=$\frac{3}{5}\sqrt{10}$,
∴RF=$\frac{4}{5}$$\sqrt{10}$,
∵∠AHB=∠AFB,
∴△BAH∽△ARF,
∵AB:AH:BH=AR:RF:AF=3:4:5,
∵AB=2,
∴AH=$\frac{8}{3}$,BH=$\frac{10}{3}$,
∴AH+BH=6.
(3)如图3中,过F、G分别作FM⊥AB于M,GN⊥AD于N,则△FME∽△GNH,
∴$\frac{EF}{GH}$=$\frac{FM}{GN}$=$\frac{3}{2}$,设OF=9x,OE=6x,则GO=6x,OH=4x,
∴S阴=S△FOG+S△EOH=$\frac{1}{2}$•6x•9x+$\frac{1}{2}$•6x•4x=39x2=$\frac{26}{15}$,
解得x=$\frac{\sqrt{10}}{15}$,
∴EF=15x=$\sqrt{10}$,GH=10x=$\frac{2}{3}$$\sqrt{10}$.
点评 本题考查相似形综合题、矩形的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考压轴题.

| A. | $\root{3}{-8}$ | B. | 0 | C. | ($\frac{1}{3}$)-1 | D. | |-$\sqrt{3}$| |
 某运动会颁奖台如图所示,它的主视图是( )
某运动会颁奖台如图所示,它的主视图是( )| A. |  | B. |  | ||
| C. |  | D. |  |
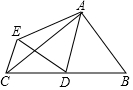 如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )
如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )| A. | 2 | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$ | D. | $\frac{7}{5}$ |