题目内容
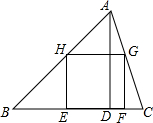如图，在△ABC中，正方形EFGH的两个顶点E、F在BC上，另两个顶点G、H分别在AC，AB上，BC=15cm，BC边上的高是10cm，则正方形的面积为考点：相似三角形的判定与性质
专题：
分析：设AD与HG交点为M，正方形EFGH的边长为x，则AM=10-x，由平行线分线成比例可得
=
，代入可求得x的值，可求得正方形的面积．
| AM |
| AD |
| HG |
| BC |
解答：解：设AD与HG交点为M，正方形EFGH的边长为xcm，则AM=10-x（cm），
∵四边形EFGH为正方形，
∴HG∥BC，
∴
=
，
即
=
，解得x=6，
∴正方形的面积为36cm2，
故答案为：36cm2．
∵四边形EFGH为正方形，
∴HG∥BC，
∴
| AM |
| AD |
| HG |
| BC |
即
| 10-x |
| 10 |
| x |
| 15 |
∴正方形的面积为36cm2，
故答案为：36cm2．
点评：本题主要考查平行线分线段成比例及正方形的性质，由条件得到
=
是解题的关键．
| AM |
| AD |
| HG |
| BC |
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
如图，要焊接一个高为3.5m，底角为32°的人字形钢架（等腰三角形），约需多长的钢材？（精确到0.01m）在数轴上与表示-3的点的距离等于5的点所表示的数是（ ）
| A、-8和2 | B、8和-2 |
| C、-8和-2 | D、8和2 |
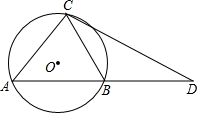如图，A、C为⊙O上两点，DA交⊙O于点B，连接AC、BC，若∠DCB=∠A，直线CD与⊙O相切吗？证明你的结论．