题目内容
在△ABC中,∠B=60°,∠C=45°,BC=20,求△ABC的面积.
考点:解直角三角形
专题:
分析:过A作AD⊥BC于D,利用直角三角形的性质求得AD的长.已知BC的长,根据三角形的面积公式即可求得其面积.
解答: 解:过A作AD⊥BC于D,
解:过A作AD⊥BC于D,
在Rt△ADC中,∵∠CDA=90°,∠C=45°,
∴∠CAD=45°,
∴AD=CD.
在Rt△ABD中,∵∠BDA=90°,∠B=60°,
∴∠BAD=30°,
∴BD=
AD.
∵BC=BD+CD=
AD+AD=20,
∴AD=30-10
,
∴S△ABC=
BC×AD=
×20×(30-10
)=300-100
.
答:△ABC的面积为300-100
.
 解:过A作AD⊥BC于D,
解:过A作AD⊥BC于D,在Rt△ADC中,∵∠CDA=90°,∠C=45°,
∴∠CAD=45°,
∴AD=CD.
在Rt△ABD中,∵∠BDA=90°,∠B=60°,
∴∠BAD=30°,
∴BD=
| ||
| 3 |
∵BC=BD+CD=
| ||
| 3 |
∴AD=30-10
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
答:△ABC的面积为300-100
| 3 |
点评:本题考查了解直角三角形,三角形的面积,锐角三角函数的定义,难度适中.准确作出辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
太阳与地球的距离大约是150000000千米,其中150000000可用科学记数法表示,下列正确的是( )
| A、15×107 |
| B、0.15×109 |
| C、1.5×108 |
| D、1.5亿 |
一元二次方程(3x-1)(-x+1)=3x-1的解是( )
| A、x=0 | ||
| B、x=1 | ||
C、x=
| ||
D、x=
|
 在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P,
在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P,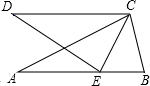 如图,把锐角△ABC绕点C顺时针旋转至△CDE处,且点E恰好落在AB上,若∠ECB=40°,则∠AED=
如图,把锐角△ABC绕点C顺时针旋转至△CDE处,且点E恰好落在AB上,若∠ECB=40°,则∠AED=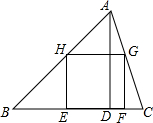 如图,在△ABC中,正方形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC,AB上,BC=15cm,BC边上的高是10cm,则正方形的面积为
如图,在△ABC中,正方形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC,AB上,BC=15cm,BC边上的高是10cm,则正方形的面积为