题目内容
已知二次函数y=x2-x-3和一次函数y=x+b有一个公共点(即相切),求出b的值.
考点:二次函数的性质
专题:
分析:根据抛物线与直线的交点问题得到△=(-2)2-4×(-b-3)=0,然后解不等式即可.
解答:解:由题意得:
,
整理得:x2-2x-b-3=0,
∵二次函数y=x2-x-3和一次函数y=x+b有一个公共点(即相切),
∴△=(-2)2-4×(-b-3)=0,
解得:b=-4.
|
整理得:x2-2x-b-3=0,
∵二次函数y=x2-x-3和一次函数y=x+b有一个公共点(即相切),
∴△=(-2)2-4×(-b-3)=0,
解得:b=-4.
点评:本题考查了二次函数的性质,解题的关键是了解抛物线与直线相切就是直线与抛物线有唯一的公共点,难度不大.

练习册系列答案
相关题目
太阳与地球的距离大约是150000000千米,其中150000000可用科学记数法表示,下列正确的是( )
| A、15×107 |
| B、0.15×109 |
| C、1.5×108 |
| D、1.5亿 |
根据专家估计,开县汉丰湖蓄水量约为8000万立方米,下列说法正确的是( )
| A、精确到个位,有一个有效数字 |
| B、精确到万位,有四个有效数字 |
| C、精确到千位,有四个有效数字 |
| D、精确到百位,有一个有效数字 |
一元二次方程(3x-1)(-x+1)=3x-1的解是( )
| A、x=0 | ||
| B、x=1 | ||
C、x=
| ||
D、x=
|
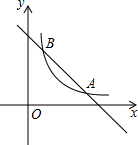 如图,直线y=-x+5与双曲线y=
如图,直线y=-x+5与双曲线y= 在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P,
在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P,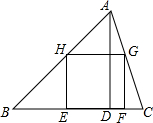 如图,在△ABC中,正方形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC,AB上,BC=15cm,BC边上的高是10cm,则正方形的面积为
如图,在△ABC中,正方形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC,AB上,BC=15cm,BC边上的高是10cm,则正方形的面积为