题目内容
 如图,要焊接一个高为3.5m,底角为32°的人字形钢架(等腰三角形),约需多长的钢材?(精确到0.01m)
如图,要焊接一个高为3.5m,底角为32°的人字形钢架(等腰三角形),约需多长的钢材?(精确到0.01m)考点:解直角三角形的应用
专题:
分析:利用锐角三角函数关系分别得出AC,AD的长,进而求出即可.
解答:解:如图所示:DC=3.5,∠A=∠B=32°,
故sin32°=
,
∴AC=DC÷sin32°≈6.605(m),
tan32°=
,
故AD=CD÷tan32°≈5.601(m),
则AB=11.202m,
故AC+BC+CD+AB=11.202+13.21+3.5≈27.91(m).
答:约需27.91m的钢材.
故sin32°=
| CD |
| AC |
∴AC=DC÷sin32°≈6.605(m),
tan32°=
| CD |
| AD |
故AD=CD÷tan32°≈5.601(m),
则AB=11.202m,
故AC+BC+CD+AB=11.202+13.21+3.5≈27.91(m).
答:约需27.91m的钢材.
点评:此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键.

练习册系列答案
相关题目
根据专家估计,开县汉丰湖蓄水量约为8000万立方米,下列说法正确的是( )
| A、精确到个位,有一个有效数字 |
| B、精确到万位,有四个有效数字 |
| C、精确到千位,有四个有效数字 |
| D、精确到百位,有一个有效数字 |
 观察二次函数y=ax2+bx+c的图象.你认为其中错误的是( )
观察二次函数y=ax2+bx+c的图象.你认为其中错误的是( )| A、a<0 |
| B、c=0 |
| C、函数的最小值为-3 |
| D、当x<0时,y>0 |
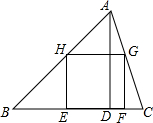 如图,在△ABC中,正方形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC,AB上,BC=15cm,BC边上的高是10cm,则正方形的面积为
如图,在△ABC中,正方形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC,AB上,BC=15cm,BC边上的高是10cm,则正方形的面积为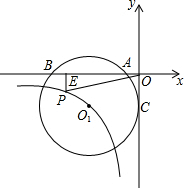 如图,⊙O1与y轴切于点C(0,-2),与x轴负半轴交于A、B两点,A(-1,0),双曲线y=
如图,⊙O1与y轴切于点C(0,-2),与x轴负半轴交于A、B两点,A(-1,0),双曲线y= 如图,已知?ABCD中,E是AB边上一点,且AE:EB=1:2,F是AD中点,则EO:OC=
如图,已知?ABCD中,E是AB边上一点,且AE:EB=1:2,F是AD中点,则EO:OC=