题目内容
如图,图①中圆与正方形各边都相切,设这个圆的周长为C1;图②中的4个圆的半径相等,并依次外切,且与正方形的边相切,设这4个圆的周长和为C2;图③中的9个圆的半径相等,并依次外切,且与正方形的边相切,设这9个圆的周长和为C3…依此规律,当正方形的边长为2时,C1+C2+C3+…+C99+C100= .


考点:相切两圆的性质
专题:规律型
分析:先从图中找出每个图中圆的面积,从中找出规律,再计算周长和.
解答:解:根据图形发现:
第一个图中,圆的周长为2π;
第二个图中,所有圆的周长之和是4π;
依此类推,则第100个图中所有圆的周长之和为200π,
∴C1+C2+C3+…+C99+C100
=2π×1+2π×2+2π×3+2π×4+…+2π×99+2π×100
=2π(1+2+3+4+…+99+100)
=10100π.
故答案为:10100π.
第一个图中,圆的周长为2π;
第二个图中,所有圆的周长之和是4π;
依此类推,则第100个图中所有圆的周长之和为200π,
∴C1+C2+C3+…+C99+C100
=2π×1+2π×2+2π×3+2π×4+…+2π×99+2π×100
=2π(1+2+3+4+…+99+100)
=10100π.
故答案为:10100π.
点评:本题考查了相切两圆的性质,观察图形,即可发现这些图中,每一个图中的所有的圆面积和都相等.

练习册系列答案
相关题目
 如图,AB是半圆O的直径,AE为弦,C为
如图,AB是半圆O的直径,AE为弦,C为
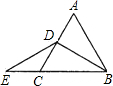 已知:如图,△ABC是等边三角形,BD是AC边上的高,延长BC到E,使CE=CD.求证:点D在BE的垂直平分线上.
已知:如图,△ABC是等边三角形,BD是AC边上的高,延长BC到E,使CE=CD.求证:点D在BE的垂直平分线上. 如图,一根5m长的绳子,一端拴在柱子上,另一端栓着一只羊,请画出羊的活动区域.
如图,一根5m长的绳子,一端拴在柱子上,另一端栓着一只羊,请画出羊的活动区域. 如图,B地在A地的正东方向,两地相距
如图,B地在A地的正东方向,两地相距