题目内容

3．把方程（x-$\sqrt{5}$）（x+$\sqrt{5}$）+（2x-1）2=0化做一元二次方程的一般形式5x2-4x-4=0．

分析 方程利用平方差公式及完全平方公式化简，整理即可得到一般形式．

解答 解：方程整理得：x2-5+4x2-4x+1=0，即5x2-4x-4=0，
故答案为：5x2-4x-4=0

点评 此题考查了一元二次方程的一般形式，一元二次方程的一般形式是：ax2+bx+c=0（a，b，c是常数且a≠0）特别要注意a≠0的条件．这是在做题过程中容易忽视的知识点．在一般形式中ax2叫二次项，bx叫一次项，c是常数项．其中a，b，c分别叫二次项系数，一次项系数，常数项．

练习册系列答案
相关题目
13．将x4-2x2+1因式分解的最终结果是（x-1）2（x+1）2．
14．定义运算a?b=a（1-b），下面给出的关于这种运算的四个结论中正确的是（　　）
A．2?（-2）=-4B．a?b=b?aC．（-2）?2=2D．若a?b=0，则a=0
11．-$\frac{1}{3}$的相反数是（　　）
A．3B．$\frac{1}{3}$C．-3D．-$\frac{1}{3}$
18．现有点数为2，3，4，5的四张扑克牌背面朝上，洗匀后，从中任意抽出两张牌，这两张牌上的数字之和能被3整除的概率是$\frac{1}{3}$．
3．（1）如图（1）在△ABC中，点D、E、Q分别在AB、AC、BC上，且DE∥BC，AQ交DE于点P，求证：$\frac{DP}{BQ}=\frac{PF}{QC}$．
（2）如图（2）在△ABC中，∠BAC=90°，AB=AC=1，正方形DEFG的四个顶点在△ABC的边上，连接AG、AF分别交DE于M、N两点，求MN的长．
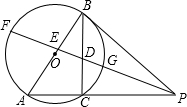10．已知：如图AB是⊙O的直径，PB切⊙O于点B，PA交⊙O于点C，PF分别交AB、BC于E、D，交⊙O于F、G，且BE、BD恰好是关于x的方程x2-6x+（m2+4m+13）=0（其中m为实数）的两根．
（1）求证：△PBC∽△BAC；
（2）求证：PF平分∠APB；
（3）若GE•EF=6$\sqrt{3}$，求∠PBC的度数．
7．阅读材料：
关于x的方程：
x+$\frac{1}{x}=c+\frac{1}{c}$的解为：x1=c，x2=$\frac{1}{c}$
x-$\frac{1}{x}=c-\frac{1}{c}$（可变形为x+$\frac{-1}{x}=c+\frac{-1}{c}$）的解为：x1=c，x2=$\frac{-1}{c}$
x+$\frac{2}{x}=c+\frac{2}{c}$的解为：x1=c，x2=$\frac{2}{c}$
x+$\frac{3}{x}=x+\frac{3}{c}$的解为：x1=c，x2=$\frac{3}{c}$
…
根据以上材料解答下列问题：
（1）①方程x+$\frac{1}{x}=2+\frac{1}{2}$的解为${x}_{1}=2，{x}_{2}=\frac{1}{2}$
②方程x-1+$\frac{1}{x-1}$=2+$\frac{1}{2}$的解为${x}_{1}=3，{x}_{2}=\frac{3}{2}$
（2）解关于x方程：x-$\frac{3}{x-2}=a-\frac{3}{a-2}$（a≠2）
8．先化简再计算：$\frac{{{x^2}-1}}{{{x^2}+x}}$÷（x-$\frac{2x-1}{x}$），其中x=$\sqrt{5}$+1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网