Question

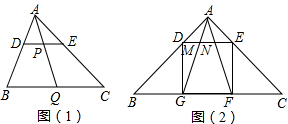
3．（1）如图（1）在△ABC中，点D、E、Q分别在AB、AC、BC上，且DE∥BC，AQ交DE于点P，求证：$\frac{DP}{BQ}=\frac{PF}{QC}$．
（2）如图（2）在△ABC中，∠BAC=90°，AB=AC=1，正方形DEFG的四个顶点在△ABC的边上，连接AG、AF分别交DE于M、N两点，求MN的长．

Answer 1

分析 （1）可证明△ADP∽△ABQ，△ACQ∽△ADP，从而得出$\frac{DP}{BQ}$=$\frac{PE}{QC}$；
（2）根据三角形的面积公式求出BC边上的高$\frac{\sqrt{3}}{2}$，根据△ADE∽△ABC，求出正方形DEFG的边长$\frac{\sqrt{2}}{3}$，根据$\frac{MN}{GF}$等于高之比即可求出MN．

解答 （1）证明：在△ABQ和△ADP中，
∵DP∥BQ，
∴△ADP∽△ABQ，
∴$\frac{DP}{BQ}=\frac{AP}{AQ}$，
同理在△ACQ和△APE中，$\frac{EP}{CQ}$=$\frac{AP}{AQ}$，
∴$\frac{DP}{BQ}$=$\frac{PE}{QC}$．

（2）解：作AQ⊥BC于点Q．
∵BC边上的高AQ=$\frac{\sqrt{2}}{2}$，
∵DE=DG=GF=EF=BG=CF
∴DE：BC=1：3
又∵DE∥BC，
∴AD：AB=1：3，
∴AD=$\frac{1}{3}$，DE=$\frac{\sqrt{2}}{3}$，
∵DE边上的高为$\frac{\sqrt{2}}{6}$，MN：GF=$\frac{\sqrt{2}}{6}$：$\frac{\sqrt{2}}{2}$，
∴MN：$\frac{\sqrt{2}}{3}$=$\frac{\sqrt{2}}{6}$：$\frac{\sqrt{2}}{2}$，
∴MN=$\frac{\sqrt{2}}{9}$．

点评 本题考查了相似三角形的判定和性质以及正方形的性质，是一道综合题目，难度较大，作辅助线AQ⊥BC是解题的关键．