题目内容
7.阅读材料:关于x的方程:
x+$\frac{1}{x}=c+\frac{1}{c}$的解为:x1=c,x2=$\frac{1}{c}$
x-$\frac{1}{x}=c-\frac{1}{c}$(可变形为x+$\frac{-1}{x}=c+\frac{-1}{c}$)的解为:x1=c,x2=$\frac{-1}{c}$
x+$\frac{2}{x}=c+\frac{2}{c}$的解为:x1=c,x2=$\frac{2}{c}$
x+$\frac{3}{x}=x+\frac{3}{c}$的解为:x1=c,x2=$\frac{3}{c}$
…
根据以上材料解答下列问题:
(1)①方程x+$\frac{1}{x}=2+\frac{1}{2}$的解为${x}_{1}=2,{x}_{2}=\frac{1}{2}$
②方程x-1+$\frac{1}{x-1}$=2+$\frac{1}{2}$的解为${x}_{1}=3,{x}_{2}=\frac{3}{2}$
(2)解关于x方程:x-$\frac{3}{x-2}=a-\frac{3}{a-2}$(a≠2)
分析 (1)①本题可根据给出的方程的解的概念,来求出所求的方程的解.
②本题可根据给出的方程的解的概念,来求出所求的方程的解.
(2)本题要求的方程和题目给出的例子中的方程形式不一致,可先将所求的方程进行变形.变成式子中的形式后再根据给出的规律进行求解.
解答 解:(1)①方程x+$\frac{1}{x}=2+\frac{1}{2}$的解为:${x}_{1}=2,{x}_{2}=\frac{1}{2}$;
②根据题意得;x-1=2,x-1=$\frac{1}{2}$,
解得:${x}_{1}=3,{x}_{2}=\frac{3}{2}$
故答案为:①${x}_{1}=2,{x}_{2}=\frac{1}{2}$;②${x}_{1}=3,{x}_{2}=\frac{3}{2}$.
(2)两边同时减2变形为x-2-$\frac{3}{x-2}$=a-2-$\frac{3}{a-2}$,
解得:x-2=a-2,x-2=$\frac{-3}{a-2}$
即x1=a,${x}_{2}=\frac{2a-7}{a-2}$.
点评 本题考查了分式方程的解,要注意给出的例子中的方程与解的规律,还要注意套用列子中的规律时,要保证所求方程与例子中的方程的形式一致.

练习册系列答案
相关题目
12. 如图,在△ABC中,BC边上的高是、在△BCE中,BE边上的高、在△ACD中,AC边上的高分别是( )
如图,在△ABC中,BC边上的高是、在△BCE中,BE边上的高、在△ACD中,AC边上的高分别是( )
 如图,在△ABC中,BC边上的高是、在△BCE中,BE边上的高、在△ACD中,AC边上的高分别是( )
如图,在△ABC中,BC边上的高是、在△BCE中,BE边上的高、在△ACD中,AC边上的高分别是( )| A. | AF、CD、CE | B. | AF、CE、CD | C. | AC、CE、CD | D. | AF、CD、CE |
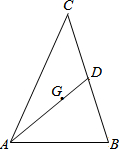 如图,G是△ABC的重心,连接AG并延长交BC于D,已知AG=2$\sqrt{3}$+2,∠BAD=45°,∠B=75°,则BC=12.
如图,G是△ABC的重心,连接AG并延长交BC于D,已知AG=2$\sqrt{3}$+2,∠BAD=45°,∠B=75°,则BC=12.