题目内容
13.解下列方程组(1)$\left\{\begin{array}{l}{x=y+1}\\{2x-y=3}\end{array}\right.$
(2)$\left\{\begin{array}{l}{3x-y=2}\\{x+4y=-21}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x=y+1①}\\{2x-y=3②}\end{array}\right.$,
把①代入②得:2y+2-y=3,
解得:y=1,
把y=1代入①得:x=2,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{3x-y=2①}\\{x+4y=-21②}\end{array}\right.$,
①×4+②得:13x=-13,
解得:x=-1,
把x=-1代入①得:y=-5,
则方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=-5}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.计算(3x-1)(1-3x)结果正确的是( )
| A. | 9x2-1 | B. | 1-9x2 | C. | -9x2+6x-1 | D. | 9x2-6x+1 |
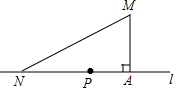 如图,我校(点M)距公路(直线l)的距离(MA)为1km,在公路上距我校2km处有一车站(点N),我校拟在公路上建一个公交车停靠站(点P),以便于我校职工乘车上下班,要求停靠站到我校与车站的距离相等,请问:停靠站应建在什么位置?并计算停靠站到车站的距离.
如图,我校(点M)距公路(直线l)的距离(MA)为1km,在公路上距我校2km处有一车站(点N),我校拟在公路上建一个公交车停靠站(点P),以便于我校职工乘车上下班,要求停靠站到我校与车站的距离相等,请问:停靠站应建在什么位置?并计算停靠站到车站的距离.