题目内容
13.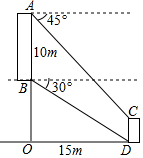 如图,从坡上建筑物AB观测坡底建筑物CD.从A点测得C点的俯角为45°,从B点测得D点的俯角为30°.已知AB的高度为10m,AB与CD的水平距离是OD=15m,则CD的高度为($5\sqrt{3}-5$)m(结果保留根号)
如图,从坡上建筑物AB观测坡底建筑物CD.从A点测得C点的俯角为45°,从B点测得D点的俯角为30°.已知AB的高度为10m,AB与CD的水平距离是OD=15m,则CD的高度为($5\sqrt{3}-5$)m(结果保留根号)
分析 根据题意作出合适的辅助线,然后根据锐角三角函数即可求得CD的长,本题得以解决.
解答  解:作CE⊥AO于点E,如右图所示,
解:作CE⊥AO于点E,如右图所示,
∵CE⊥AO,∠FAC=45°,OD=15m,
∴∠CAE=45°,CE=15m,
∴AE=15m,
∵AB=10m,
∴BE=5m,
∵∠BOD=90°,∠BDO=30°,OD=15m,
∴BO=15×tan30°=15×$\frac{\sqrt{3}}{3}$=5$\sqrt{3}$m,
∴EO=BO-BE=5$\sqrt{3}-5$,
∴CD=EO=5$\sqrt{3}-5$,
故答案为:($5\sqrt{3}-5$).
点评 本题考查解直角三角形的应用-仰角俯角问题,解答本题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数解答.

练习册系列答案
相关题目
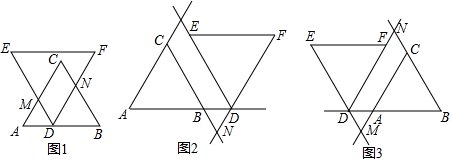
1. 如图所示,几何体的主视图是( )
如图所示,几何体的主视图是( )
 如图所示,几何体的主视图是( )
如图所示,几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
8.下列各数是无理数的是( )
| A. | $\sqrt{4}$ | B. | 2.2020020002 | C. | $\root{3}{9}$ | D. | -1 |
3. 如图,△ABC的角平分线相交于点P,∠BPC=125°,则∠A的度数为( )
如图,△ABC的角平分线相交于点P,∠BPC=125°,则∠A的度数为( )
 如图,△ABC的角平分线相交于点P,∠BPC=125°,则∠A的度数为( )
如图,△ABC的角平分线相交于点P,∠BPC=125°,则∠A的度数为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
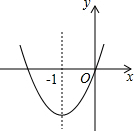 如图,已知经过原点的抛物线y-ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:①ab>0,②a+b+c>0,③当-2<x<0时,y<0,正确的结论是①②③.
如图,已知经过原点的抛物线y-ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:①ab>0,②a+b+c>0,③当-2<x<0时,y<0,正确的结论是①②③.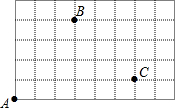 如图,每个小正方格都是边长为1个单位长度的正方形,如果用(0,0)表示A点的位置,用(3,4)表示B点的位置,那么C点的位置可表示为(6,1).
如图,每个小正方格都是边长为1个单位长度的正方形,如果用(0,0)表示A点的位置,用(3,4)表示B点的位置,那么C点的位置可表示为(6,1).